Physical Science Laboratory
Ā@With advanced semiconductor growth techniques, it is possible to prepare
two layers of two-dimensional electron gases separated by a thin tunnel barrier
of a few nanometer thickness. Such systems, referred to as bilayer electron
systems, allow one to tune the strengths of electron-electron interactions
and tunneling between two layers, and exhibit novel physical properties that
can not be achieved in a single layer. In particular, perpendicular magnetic
fields enhance the electron-electron interactions by quenching the kinetic
energy of electrons into discrete Landau levels. In this study, we reveal
that the electron system exhibits a ferromagnetic order in particular situations
when two Landau levels coincident at the Fermi energy (EF)
are regarded as up and down states of virtual spin (pseudospin).
Ā@We have fabricated a novel GaAs/AlGaAs quantum-well (QW) structure having
both front gate and n+-GaAs Back gate to control the total electron
density, ns, and the potential symmetry independently
[1, 2]. We employ a 40-nm wide single QW, which involves two occupied subbands
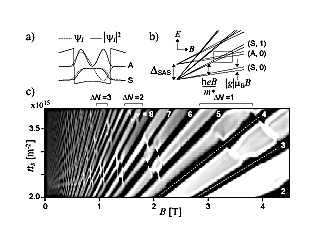
with symmetric (S) and antisymmetric (A) wave functions and therefore behaves
effectively like a bilayer [Fig. 1(a)]. When a perpendicular magnetic field,
B, is applied, two sets of Landau levels originate from the two subbands,
giving rise to various level crossings [Fig. 1(b)]. The energy diagram and
the level crossings can be confirmed by measuring the magnetoresistance as
a function of B and ns while keeping the
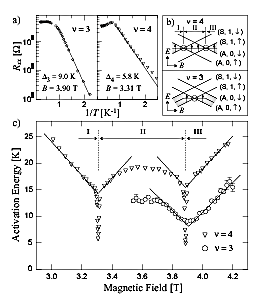
QW potential symmetric [Fig. 1(c)]. Activation measurements reveal that, at
Landau level filling factor É“ = 3 and 4, there is a finite energy gap even
when two levels cross at EF [Fig. 2(a),(b),(c)].
This energy gap shows the existence of a ferromagnetic order in the electron
system, which suppresses the pseudospin flip and hence a dissipative current.
This is a new class of integer quantized Hall effect which relies solely on
interactions.
[1] K. Muraki, N. Kumada, T. Saku, and Y. Hirayama, Jpn. J. Appl. Phys. 39 (2000) 2444.
[2] K. Muraki, T. Saku, and Y. Hirayama, Phys. Rev. Lett. 87 (2001) 196801.
 |
 |
||||
|
|