Materials Science Laboratory
@It is difficult to detect the magnetization of a single micro-magnet even
by using a high sensitive susceptibility-meter; therefore, ensemble averaged
magnetization processes is measured in an array including several thousand
micro-structured magnets. We have shown that a fringe-field-induced local
Hall effect (LHE) device can detect the magnetization process of a single
micro-structured magnet [1]. It has been predicted that a flux closure state
(vortex state) is stable in ferromagnetic small ring structures. In the vortex
state, almost no stray field is generated, that offers a potential application
for high integration of the magnetoresistive random access memory (MRAM).
We have investigated the magnetization processes of micro-structured ferromagnetic
rings using the LHE device and have found that the magnetic transition strongly
depends on the inner diameter of the ring.
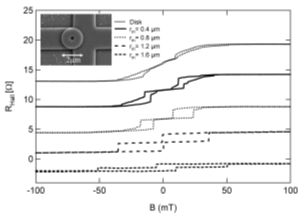
@The inset of Fig. 1 shows an SEM image of a fabricated sample. A cross-shape
is a semiconductor Hall device. A NiFe micro-structured ferromagnetic ring
is placed near the Hall cross to detect a fringe field. An external magnetic
field is applied in parallel to the semiconductor two-dimensional electron
gas in order that it does not affect the Hall resistance. Figure 1 shows hysteresis
loops of the Hall resistance. The outer diameter of the rings is fixed to
2.0 Êm, and the inner diameter is varied from 0 (Disk) to 1.6 Êm in steps
of 0.4 Êm. We observed a systematic change in the hysteresis loops by increasing
the inner diameter. For narrow rings, sharp transitions from the so-called
gonionh state to the gvortexh state were observed. In rings with smaller inner
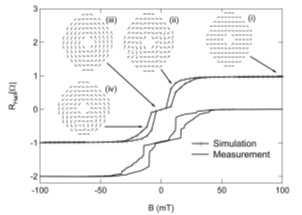
diameter, the transitions are broad and more complex [2]. A comparison between
the hysteresis loop of the Hall resistance of a 0.4 Êm-diameter ring and numerical
calculation is shown in Fig. 2. Starting from the onion state (i), the ring
reversibly enters a wave-like state (ii). The global vortex state (iii) is
then irreversibly reached and forms a stable configuration that produces a
plateau in the hysteresis. Via an irreversible transition into a single local
vortex state (iv), the saturation configuration is reached again. The measured
Hall resistance loop is well reproduced by the numerical simulation.
@These results indicate that the transition field to the vortex state can
be controlled by the inner diameter.
[1] J. Nitta, et al. Jpn. J. Appl. Phys. 41 (2002) 2479.
[2] M. Steiner and J. Nitta, Appl. Phys. Lett. 84 (2004)
939.
 |
 |
||||
|
|