Quantum cryptography, which provides an unconditionally secured secret key based on quantum mechanics, is extensively studied. Although several schemes have been proposed, each has problems with respect to suitability for fiber transmission, or operation stability, or data rate. This study proposes and demonstrates a novel quantum cryptography scheme, called differential-phase-shift quantum key distribution, which can realize a stable high-speed system.
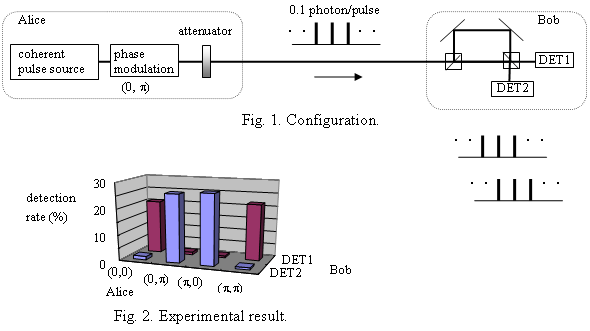
　Fig. 1 shows the configuration of the proposed system. The transmitter (called Alice) randomly phase-modulates a coherent pulse train and sends out it with a power level of 0.1 photon/pulse. The receiver (called Bob) detects the pulses after a one-bit delayed interferometer. In the detection, DET1 clicks for 0 phase difference between two sequential pulses, and DET2 clicks for π phase difference. Here, the click occurs once in ten time-slots (Detection time is probabilistic) since the transmitted power is 0.1 photon/pulse. After the transmission, Bob discloses detection instances to Alice, who can identify, from her modulation data, which detector clicked at corresponding instances. Provided that the DET1 click represents “0” and the DET2 click “1”, Alice and Bob share an identical bit string, which can be a secret key because the bit information itself has not been leaked to the outside. The system consists of a simple phase modulation scheme and a passive interferometer, and thus can realize stable operation at a high data rate.
　We carried out an experiment to demonstrate the above scheme. A 0.8-μm LD light was phase-modulated, attenuated, and then was photon-detected after an open-space interferometer. The result is shown in Fig. 2. Proper correlation between Alice and Bob was obtained, which confirmed the operation.

[1] K. Inoue, E. Waks, and Y. Yamamoto, Phys. Rev. Lett. 89 (2002) 037902.
[2] K. Inoue, E. Waks, and Y. Yamamoto, Phys. Rev. A 68 (2003) 022317.