Physical Science Laboratory1, NTT Photonics Labs. 2, NTT Electronics3, Univ. of Tokyo4
Crystals have periodicity and translational symmetry. But there exist a
certain class of structures called quasicrystals that do not posses periodicity
nor translational symmetry, but have long-range order and rotational symmetry.
Quasicrystals have bandgap and density of states in a similar way to crystals,
but some important concepts such as band structures, Bloch theorem, Brillouin
zone cannot be defined. Concerning crystals, it has been known that lasing
action is possible in photonic crystals having optical gain because of some
standing wave formation at the photonic band edges. Then, what happens if
we introduce gain into photonic quasicrystals that do not have periodicity?
Is coherent lasing possible?
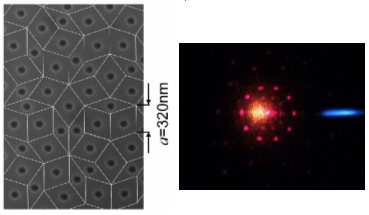
From these backgrounds, we have fabricated photonic quasicrystal lasers with
organic dye for the first time. [1] Our quasicrystals have so-called Penrose
lattice (shown in Fig. 1(left)) exhibiting 10-fold rotational symmetry which
is inhibited in periodic crystals. By optical pumping, we observed clear lasing
action, and peculiar 10-fold rotationally symmetric spot patterns shown in
Fig. 1(right). Both of lasing wavelengths and spot patterns sensitively depend
on the quasilattice constant, indicating that lasing is due to the quasiperiodicity.
Sharp spot patterns also indicate that lasing occurs by delocalized coherent
modes inside the quasicrystal.
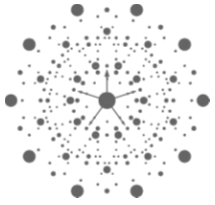
Since we cannot use conventional band theory for quasicrystal, we instead
used their reciprocal lattice to analyze the lasing action, and successfully
explained the observed lasing wavelengths and spot patterns quantitatively.
The reciprocal lattice of quasicrystals are very unique comparing to crystals
one. The reciprocal lattice of crystals have a Brillouin zone and any points
outside it are equivalent to some points inside it. In the case for quasicrystals,
all of them are basically non-equivalent, and thus a wide variety of lasing
modes can exist. This uniqueness of the reciprocal lattice is most distinguishable
feature of quasicrystal lasers. In fact, lasing action in periodic photonic
crystals is restricted from the limitation of periodicity, but quasicrystal
lasers are free from those restrictions.
[1] M. Notomi, H. Suzuki, T. Tamamura, K. Edagawa, Phys. Rev. Lett. 92 (2004) 123906.
 |
 |
||||
|
|