Kazuyuki Uchida, Hiroyuki Kageshima and Hiroshi Inokawa
Physical Science Laboratory
It is expected that novel physics appear in nano-scale devices, while many studies are needed to clarify such physics. For example, it is not clear what happens on the capacitance characteristics, one of the fundamental characteristics of FETs (field effect transistors), when the device size is decreased in nano-scale. We developed a new method, the EFED (enforced Fermi-energy difference) method, with which we can calculate the capacitance characteristics from first principles if only we provide the atomic distribution and the element type for each atom. We then applied the method for nano-capacitors and discussed physics in the nano-capacitance dependence on the material.
Since only the most stable electronic states are calculated in usual
first-principles methods, electrons distributed extensively in the system
to screen the positive charges of the atomic nucleus. To calculate capacitance
characteristics, the electrons should be localized. We divided the system’s
space into two, and applied external virtual work on the two spaces to
redistribute electrons. We minimize the total free energy for the electrons
with this additional work and obtained a Schrödinger equation for
the electrons to polarize in the system. This is the principle of our EFED
method.
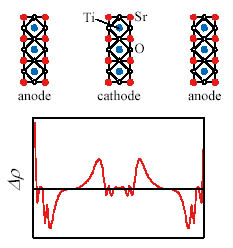
We applied this method on a nano-capacitor and calculated the dependence
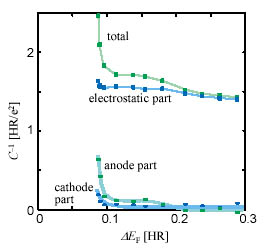
of the differencial capacitance on the Fermi energy difference. The system
consists of repeated-parallel-planes with 3-atomic-layers films of SrTiO3(001). The inverse of the differencial capacitance is shown in the vertical
axis of Fig. 2. Classical capacitance of parallel planes is written as
C = eS/d, which means that it depends only on the distance of the electrodes, d, and the dielectric constant of the material between the electrodes, e.
In nano-structure capacitors, however, the electronic states of each electrode
prefer to be discretized because of space quantization and the Coulomb
interaction between the electrons. Therefore, the capacitance strongly
depends on the difference of the Fermi energies as well as on the distance
of the electrodes and the material between the electrodes.
[1] K. Uchida, et al., e-J. Surf. Sci. & Nanotechnol. 3 (2005) 453.
 |
 |
||||
|
|