Optical Science Laboratory
Topology of an electron wavefunction in artificial structures is determined
by the structural parameters if the disturbance of the electron can be
neglected [1]. The topology of an exciton wavefunction, however, heavily
depends on the delocalized feature of the relative motion of an electron-hole
pair making an exciton as well as the structural parameters. We focused
our eyes to this situation and investigate the topological aspects of the
exciton in nanotube structures [2].
It has been demonstrated that the exciton wavefunction shows variety
of spatial distribution patterns depending on the structural parameters
of the nanotube structure. We found that the origin of the change of the
exciton wavefunction by controlling the tube circumference length comes
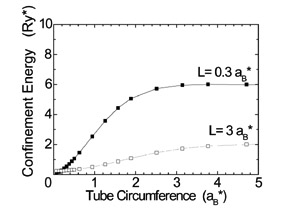
from the topological transition. As shown in Fig. 1, the kinetic energy
of the ground state exciton in nanotubes decreases monotonically when the
circumference length decreased. This is somewhat curious because smaller
confinement region yields larger confinement kinetic energy in conventional
artificial structures. The exciton wavefunction is delocalized and it is
connected in small circumference nanotubes, while the exciton wavefunction
is localized in large circumference ones. The connected wavefunction has
ring-like topology and it yields the flat wavefunction for a ground state
electron and exciton reducing the confinement energy.
We have also found that the topological transition can be controlled
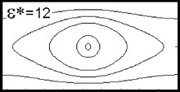
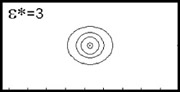
even by changing the barrier dielectric constant of the nanotubes. Figure
2 plots the ground state exciton wavefunctions on developments of two nanotubes
with different barrier dielectric constants, 12 and 3. It can be clearly
seen that the wavefunction of ε=12 case is delocalized in the direction of circumference (horizontal in
the figure) and connected, while the wavefunction of ε=3 case is localized in a small area and disconnected. This implies that
we can control the topology of the exciton wavefunction simply by changing
the dielectric constant or other material parameters. We expect the control
of the artificial structure to provide a novel guiding principle for creating
functional devices through the topological control of excitons.
[1] M. Kumagai and T. Ohno, Solid State Commun. 83 (1992) 837.
[2] M. Kumagai, et al., Solid State Commun. 145 (2008) 154.
 |
  |
|||||
|
|