Physical Science Laboratory, *Tokyo University of Science
The readout of a qubit state is a typical indirect quantum measurement
that is performed with a probe. We report here our successful theoretical
analysis of a superconducting qubit readout with a Josephson bifurcation
amplifier (JBA) as the probe. We also use this readout method in our experiments.
JBA is a non-linear oscillator, which has two resonance modes (high-amplitude
mode E state, and low-amplitude mode G state). Small changes in operational parameters (driving frequency, driving
amplitude, etc.) determine which mode is realized. When we make a JBA interact
with a qubit, the resulting JBA state reflects a small change in the effective
operational conditions depending on the qubit state. So, we can readout
the qubit state (microscopic information) as the realized JBA state (macroscopic
information) [1]. This constitutes a form of quantum signal amplification.
The JBA readout method is suitable for quantum processing because it has
almost no detrimental effect on the post-measurement qubit state. The readout
process is certainly the quantum time-evolution (quantum dynamics) of a
qubit-JBA coupled system. We have clarified the process theoretically.
In particular, we have shown how a superposed qubit is projected into one
of the measurement basis states probabilistically during this readout process
[2].
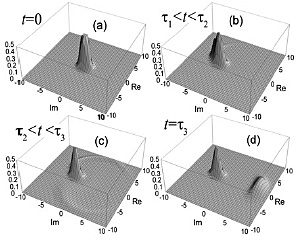
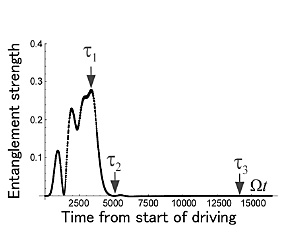
As the driving force is increased, the interaction between the qubit and
the JBA gradually increases, and the unitary evolution makes the coupled
system become an entangled state consisting of two qubit-JBA correlated
states (0<t<τ 1: see figures below). In one of them the qubit is in the excited (e) state, and the JBA is in the G state. In the other, the qubit is in the ground (g) state, and the JBA
is in the G’. As the driving force is further increased, the g-G’ pair starts to transit to g-E. At this point, the decoherence in the JBA destroys the entanglement (t~τ 2). In due cource, the coupled system becomes a mixture consisting of an
e-G and g-E pair. This means that the coupled system is now (t~τ 3) one of the two possible states although we do not know which is realized
until we perform a measurement. By judging whether the JBA state is G or E with a usual classical measurement, we can know into which state (g or e) the qubit is projected.
[1] I. Siddiqi et al., Phys. Rev. Lett. 93 (2004) 207002.
[2] H. Nakano, S. Saito, K. Semba, and H. Takayanagi, Phys. Rev. Lett.
102 (2009) 257003.
 |
 |
|||||
|
|