Optical Science Laboratory
Cold atoms trapped in optical lattices are ideal model systems for investigating
the many-body problems which have been studied for many years in condensed
matter physics. These controllable systems are thus considered as a quantum
simulator. In fact, the quantum phase transition from a metallic state
to a Mott insulating state has been successfully realized using fermionic
40K atoms in optical lattices [1]. The antiferro-magnetic (AF) transition
in the optical lattice system is a major current concern for condensed
matter physicists, because it could provide ways to elucidate the nature
of high Tc superconductors. According to the recent rapid progress in cold atom experiments,
one can expect the AF phase in optical lattice systems to be observed at
lower temperatures in the near future. This naturally motivates us to undertake
a detailed theoretical study of the properties of the AF transition in
this system. However, there was no reliable theoretical method to investigate
this issue, because the trapping potential, which is a characteristic of
optical lattice systems, makes the analysis much more complex.
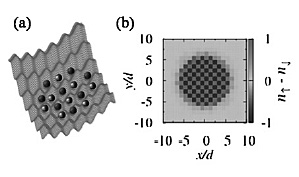
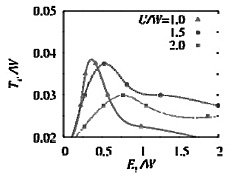
We have investigated the two-component fermionic atoms trapped in a two-dimensional (2D) optical lattice [2]. We extended the self-energy functional approach (SFA), which is known as a powerful numerical tool to analyze strongly correlated electron systems at finite temperatures. However, due to the trapping potential, it has been difficult to investigate realistic optical lattice systems using a conventional SFA algorithm. We solved this difficulty and confirmed that the extended-SFA can be successfully applied to the 2D optical lattice system. The calculated results showed reasonable agreements with the previous experimental and theoretical results [1]. Furthermore, we studied the AF transition in this 2D optical lattice system systematically. As shown in Fig. 1, below the AF transition temperature, the AF ordered region develops from the bottom of the trapping potential where the Mott insulating region appears at certain higher temperatures. Finally, we estimated the AF transition temperature (Fig. 2), and proposed a suitable parameter region for observing the AF ordered phase experimentally.
This work was partly supported by CREST of the Japan Science Technology
Agency.
[1] U. Schneider et al., Science 322 (2008) 1520; R. Jordens et al., Nature 455 (2008) 204.
[2] K. Inaba and M. Yamashita, submitted to Phys. Rev. A.
 |
 |
|||||
|
|