Physical Science Laboratory
To realize quantum memories for quantum computation, we need to establish
quantum information transfer and the generation of a photon number state
(especially a one-photon state). However it is difficult to generate a
photon number state because the method, which excites an LC resonator by
using a resonant microwave, forms a classical coherent state. So, we attempt
to generate a non-classical photon state by transferring a photon from
a superconducting qubit to an LC resonator.
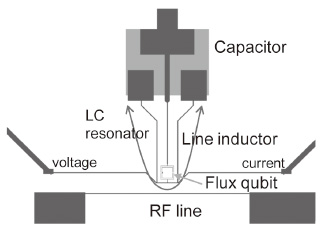
The LC resonator, which is constructed from a line inductor and a capacitor,
surrounds a superconducting flux qubit (Fig. 1). The magnetic coupling
energy between the flux qubit and the LC resonator is 360 MHz. A large
coupling energy is one of the advantages of using a superconducting qubit.
In this LC resonator and flux qubit system, we shift the external magnetic
field non-adiabatically, after realizing the excited qubit state. By tuning
the resonant condition of the LC resonator and qubit, we generate a photon
oscillation, which is called a vacuum Rabi oscillation. Time domain control
of this quantum oscillation makes it possible to transfer a photon from
a qubit to an LC resonator. By repeating this process, we can transfer
photons one by one. The ideal photon state achieved using this method becomes
the photon number state. Period time of quantum oscillation of this system
depends on the photon number, so we can obtain information about the photon
distribution of the LC resonator by analyzing the time domain oscillation.
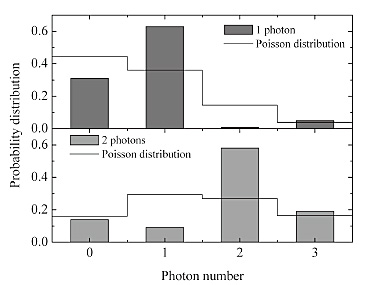
Figure 2 shows the photon distribution results when we transfer one and two photons to the LC resonator. Energy relaxation and the imperfection of the control pulses mean that this photon distribution is different from the pure photon number state. However, we succeeded in generating a non-classical photon distribution, which is clearly different from a classical Poisson distribution [1]. This is the result of using the LC resonator’s quantum characteristics, so we can expect the development of quantum memories by using high-Q resonators.
[1] K. Kakuyanagi et al., Appl. Phys. Express 3 (2010) 103101.
 |
 |
|||||
|
|