Storage and Retrieval of Quantum States in a Hybrid Quantum System
Superconducting quantum bits (qubits) are one of the most promising candidates
for a future large-scale quantum processor because of their controllability
and scalability. However the currently reported coherence times of these
has not yet reached the levels associated with those of microscopic systems
such as electron spins, nuclear spins etc. On the other hand, it is hard
to control and scale up such systems as they are well isolated from their
environment. In this context, a superconductor-spin ensemble hybrid system
has attracted considerable attention. We have utilized a nitrogen vacancy
(NV) spin ensemble in diamond to act as a quantum memory for a superconducting
flux qubit. By bonding the diamond crystal on top of a gap tunable flux
qubit [1], we had realized strong coupling between the qubit & spin
ensemble and further observed vacuum Rabi oscillations between them [2].
However we couldn’t store quantum information in the spin ensemble because
its coherence time was too short. To overcome this we applied an in-plane
magnetic field of 2.6 mT to the diamond crystal to reduce strain effects
on decoherence and thus succeeded in performing quantum memory operations
[3].
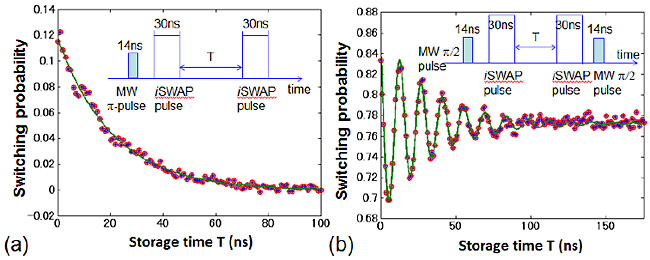
The inset of Fig. 1(a) shows a pulse sequence for storage of a single
excitation present in the flus qubit. First we detuned the qubit from the
spin ensemble and applied a microwave π pulse to prepare the qubit in the
excited state |1>qb|0>ens. Next to transfer the excitation to the spin ensemble |0>qb|1>ens, we applied an iSWAP pulse making the qubit on resonance with the spin ensemble for 30 ns. Then we keep the excitation in the spin ensemble for a storage time T and retrieved it by applying the iSWAP pulse again. Finally we measured the state of the qubit. From this experiment, a decay time of the excitation was determined as 20.8 ns (Fig. 1(a)). In a similar manner, we can store a superposition state in the spin ensemble by using two microwave π/2 pulses instead of the π pulse (Inset of Fig. 1(b)). From this Ramsey interference experiment on the spin ensemble, we could evaluate the decay time of the superposition state at 33.6 ns (Fig. 1(b)). These results show that we can store information of a population and a phase, namely an arbitrary quantum state in the spin ensemble. Our results are a significant first step to realize the long lived quantum memory and we will improve the diamond property and a coupling scheme to realize it.
This work was supported by FIRST and NICT.
- [1]
- X. Zhu, et al., Appl. Phys. Lett. 97 (2010) 102503.
- [2]
- X. Zhu, et al., Nature 478 (2011) 221.
- [3]
- S. Saito, et al., Phys. Rev. Lett. 111 (2013) 107008.
|
|
|
|