Topological Raman Band in the Carbon Nanohorn
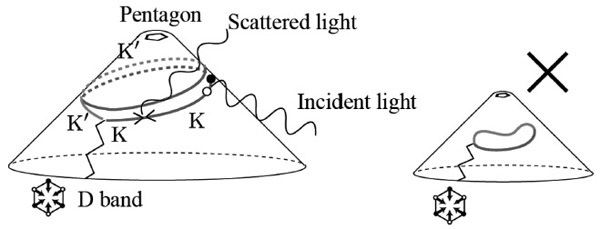
Five-membered rings (pentagons) are found throughout the honeycomb network of carbon. For example, pentagons appear in fullerenes, at the apexes of carbon nanohorns, at the junctions of carbon nanotubes, and in a flat sheet of graphene as a constituent of the Stone-Wales defect [1]. A pentagon is a topological defect, which is represented as the flux of a pseudomagnetic field that is perpendicular with respect to the graphene layer [2]. An interesting consequence of such a flux in quantum mechanics is the Aharonov-Bohm (AB) effect. However, the AB effect is usually observed at very low temperature and/or for samples essentially devoid of defects so that they maintain coherence, which prevents us from utilizing the AB effect in practical applications.
We show that a topological defect causes a special band (peak) in the Raman spectrum of a carbon nanohorn, which we call a topological Raman band [3]. A topological Raman band is excited through the AB effect for pentagons, and can be observed even at room temperature. A photo-excited "relativistic" carrier with a non-zero winding number is the key to activating a topological D Raman band (Fig. 1). A topological D band can be distinguished from the conventional D band excited at the graphene edge by its non-dispersive nature, because the selection rules for electron-phonon matrix elements are altered in an essential way by the presence of the pentagon.
- [1]
- H. W. Kroto et al., Nature 318 (1985) 162; S. Iijima et al., Nature 356 (1992) 776; S. Iijima et al., Chem. Phys. Lett. 309 (1999) 165; A. Hashimoto et al., Nature 430 (2004) 870.
- [2]
- J. González et al., Phys. Rev. Lett., 69 (1992) 172; P. E. Lammert et al., Phys. Rev. Lett., 85 (2000) 5190; K. Sasaki et al., Prog. Theor. Phys. 113 (2005) 463.
- [3]
- K. Sasaki et al., Phys. Rev. Lett., 111 (2013) 116801.
|
|
|
|