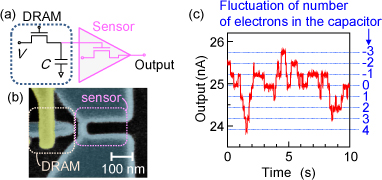
The performance of integrated circuits used in a range of electronic devices has been improved by downsizing transistors in the circuits. Such downsizing, however, increases the noise-related degradation of circuit performance, and the importance of an analysis of noise with single-electron resolution has therefore been growing. Indeed, random telegraph noise originating from single-electron trapping in a transistor gives rise to errors in memory circuits composed of small transistors. In this work, using a dynamic random access memory (DRAM), we demonstrate an analysis of thermal noise, one of the most fundamental noises in electronic devices, with a single-electron resolution.
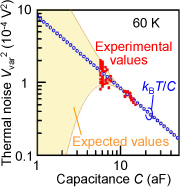
For the analysis, the DRAM is combined with a charge sensor based on a transistor [Figs. 1(a) and (b)]. Since this sensor has charge sensitivity of single-electron resolution, the number of electrons in the capacitor of the DRAM can be counted. The output signal from the sensor [Fig. 1(c)] indicates that single electrons enter and leave the capacitor randomly and thus the number of electrons in the capacitor fluctuates, which is exactly single-electron thermal noise. Using the characteristics of the sensor, we can convert the fluctuation of the number of electrons into voltage fluctuation. It is well known that according to the law of energy equipartition in which each electron has thermal energy kBT/2 on average, a variance Vvar2 of voltage fluctuation can be given by kBT/C, where kB is the Boltzmann constant, T temperature, C capacitance. Figure 2 shows the change in Vvar2 as a function of C. While Vvar2 is close to kBT/C at C > 10 aF, C smaller than 10 aF causes a deviation between Vvar2 and kBT/C. When charging energy EC (= e2/2C) for injecting one electron into the capacitor is smaller than thermal energy kBT/2, the thermal energy helps electrons in enter and leave the capacitor, which means that kBT/C or the law of energy equipartition is satisfied. On the other hand, when EC > kBT/2 at smaller C, the thermal energy is not large enough to help electrons in enter and leave the capacitor, which leads to smaller Vvar2. Additionally, voltage V applied to the DRAM can adjust the energy for injecting and rejecting one electron to be zero. This allows even small thermal energy to help one electron to enter and leave the capacitor, which makes Vvar2 larger than kBT/C. These features at EC > kBT/2 represent a deviation from the law of energy equipartition. Since our demonstration is carried with DRAM of very small size, our results are very important for all electronic devices with small dimensions.