Ultracold atom gases can be trapped in an optical lattice using lasers. The high controllability of atoms provides us with an ideal tool for investigating quantum many-body systems, such as mimicking electrons in bulk materials. Thus, the system can be regarded as a quantum simulator, which stimulates theoretical and experimental efforts to observe quantum magnetism using fermionic atoms. The Kyoto university group, led by Prof. Yoshiro Takahashi, has successfully created the Lieb optical lattice [Fig. 1(a)], which attracts much attention as mentioned below. The band structure of this two-dimensional Lieb lattice shows a dispersionless band (flat band), which may induce the exotic magnetic ordering state (flat-band ferromagnetism). The emergence of this state is exactly shown (Lieb theorem [1]), which has attracted theoretical attention. The realization of the Lieb optical lattice provides an ideal opportunity for the first observation of the flat-band ferromagnetism.
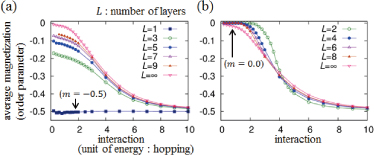
In the experiment, a multilayer Lieb optical lattice [Fig. 1(b)] (L represents the number of layers) is inevitably realized. To observe the flat-band ferromagnetism, we theoretically investigate how this multilayer structure affects magnetic ordering [2]. We reveal that the property of magnetic ordering is quite different between odd layers (L=2l-1, where l is a positive integer) and even layers (L=2l). Figure 2 shows average magnetization, which is an order parameter of the magnetic ordering, as a function of atom-atom interaction strength. For odd layers (L=2l-1), Fig. 2 (a) shows that finite magnetizations appear with quite weak interaction strength. This indicates the emergence of the flat-band ferromagnetism, which can be regarded as a generalized consequence of that on a single layer (L=1, the two-dimensional Lieb lattice mentioned above). Further, we also find the gradual change of the magnetic ordering states from the two dimensions (L=1) to the three dimensions (L→∞). This result exhibits that the flat-band magnetism, well-known for the two dimensions, appears even in the three dimensions. On the other hand, for even layers (L=2l) [Fig. 2 (b)], we reveal that magnetization develops at finite interaction strength. As L increases, this critical interaction strength decreases. Thus, in the limit of L→∞ (three dimensions), the difference between odd and even layers disappears and the flat-band magnetism appears. In experiment, a multilayer Lieb optical lattice that consists of several tens of layers will show the three-dimensional flat-band magnetism, which is revealed in our study.
This work was supported by JST-CREST and KAKENHI.