Quantum key distribution (QKD) is a way to distribute a random bit sequence, which is called a key, between a sender (Alice) and a receiver (Bob). Its striking advantage is that the leakage of the information on the key to an eavesdropper (Eve) can be arbitrary set according to Alice and Bob’s demand. In order to achieve such high security, the QKD devices must operate as the security theory requires. For instance, in the case of the most well-known protocol, BB84 [1], the phase modulator is required to apply an exact phase modulation, which is randomly chosen from 0, π/2, π, 3π/2, for each pulse. However, such exact values can never be achieved due to the imperfections in the modulator.

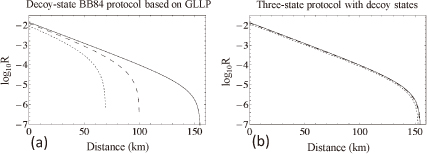
This kind of modulation error would not seem to be so problematic to affect the security, unfortunately however, this is not the case. In a typical QKD communication, due to the inevitable photon losses in the quantum channel, a single photon is detected only once out of 1000 emission pulse. Eve may exploit these losses in such a way that only when she succeeds in exploiting the modulation error, she sends out a pulse to Bob to cause the detection event. In other words, she may enlarge the effective modulation errors. This is exactly what happened in the existing theory [2]. Figure 1(a) is a plot of the key generation rate against the distance between Alice and Bob, and the solid, dashed and dotted lines respectively represent the case with perfect modulation, the modulation error case with about 3.6 degree, and the modulation error case with about 7.2 degree. One can see in the figure that the small errors have a severe impact on the achievable communication distance.

In our work [3], we have proposed a technique to drastically decrease the effect that the imperfect state preparation has on the communication distances. This is made possible by utilizing the data, which was used to be discarded in the BB84 protocol. Figure 1 (b) is the plot of the key rate against the distance based on the same experimental data as used in Fig. 1(a). The three lines are almost superposed, implying that the state preparation flaw is not problematic. Moreover, it can be concluded from our observation that sending three states is enough in the BB84 where sending four states was considered to be needed.

Our research is in part supported by FIRST and NICT.