Probing the Extended-state Width of Disorder-broadened Landau Levels in Epitaxial Graphene
Graphene is theoretically predicted to have a zero-energy Landau level, the energy width of which depends on the types of disorder; the energy width is ideally nearly zero in the presence of typical hopping disorder such as ripples, owing to protected chiral symmetry associated with graphene sublattice-symmetry. Previously, we developed transport energy-spectroscopy techniques relaying on densities of interface states involved in epitaxial graphene device [1]. Using the technique, here we report temperature dependences of the energy widths of the extended states of the zero-energy and first excited Landau levels, from which we can also deduce exponents corresponding to the critical exponents used in the quantum Hall plateau-plateau transition. The energy widths obtained from the spectroscopy technique are also compared with the energy widths deduced from the activation gap measurements [2].
Figure 1(a) shows longitudinal resistance as a function of gate voltage (Vg) and magnetic field (B). Due to the presence of the interface states in gate insulator or in SiC underneath the graphene (Fig. 1(b)), trajectories of the longitudinal-resistance peaks become parabolic, reflecting the unequally-spaced graphene Landau levels. Such a Vg-B relation enables us to deduce the energy width ∆EN of the extended states of the Nth Landau level. Figure 1(c) and (d) show temperature (T) dependences of ∆E0 and ∆E1. These show that ∆E0 and ∆E1 have similar magnitudes and are proportional to Tη with η = 0.30 - 0.31 for ∆E0 and η = 0.32 - 0.35 for ∆E1. These values are comparable to the critical components previously deduced from the plateau-plateau transition in quantum Hall regimes. Moreover, we deduced the energy widths independently using activation gap measurements. The energy width for N = 1 Landau level show a good agreement between two different types of measurement methods, while the energy width for the N = 0 Landau level obtained from activation gap measurement is larger by 30 meV than that deduced from the transport energy-spectroscopy.
Using these two different measurement techniques systematically, we demonstrate that our device include random disorder rather than typical hopping disorder such as ripples.
This work was partly supported by KAKENHI.
- [1] K. Takase, S. Tanabe, S. Sasaki, H. Hibino, and K. Muraki, Phys. Rev. B 86, 165435 (2012).
- [2] K. Takase, H. Hibino, and K. Muraki, Phys. Rev. B 92, 125407 (2015).
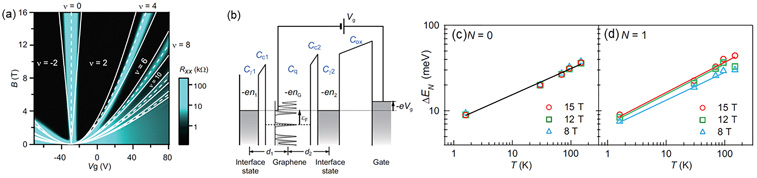
|
| Fig. 1. (a) Longitudinal resistance as a function of gate voltage (Vg) and magnetic field (B). (b) Energy diagram of graphene with interface states. Temperature dependence of ∆EN for the N = 0 Landau level (c) and N = 1 Landau level (d). |