An Entanglement Analogue in Light Cones
In relativistic spacetime, the notion of light cones is essential and nothing can travel faster than light. Thus, the path of a particle stays inside the light cone. (In what follows, we take the unit of c = 1). In this work, we drew an analogy between the structure of light cones and entanglement in quantum theory.
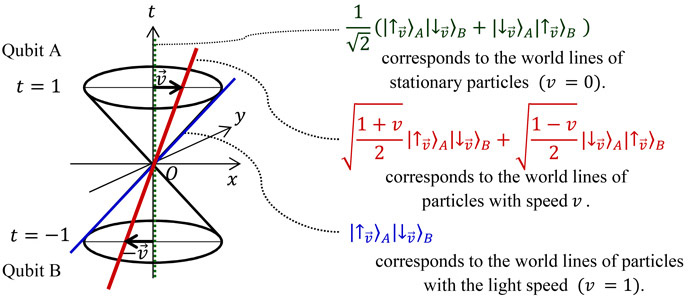
There are two parts in a light cone, the future cone and the past cone, as shown in Fig. 1. The cross sections at t = ±1 become unit spheres in three dimensions (In Fig. 1, the cross sections of the light cone in 2+1 dimensions become unit circles in two dimensions). Each unit sphere can be identified with the Bloch sphere of a qubit in quantum information theory. Thus, we introduce two imaginary qubits, one for the future and the other for the past. Considering world lines of particles with constant speeds, the directions of the particles in four dimensions can be represented by points on or inside the Bloch sphere. In other words, the directions of particles with the light speed correspond to the points on the surface of the sphere, and the directions of particles travelling slower than light correspond to the points inside the sphere.
This correspondence can be seen as the one between world lines of particles and entangled states of two imaginary qubits representing the cross sections of the light cones in the future and the past. According to this analogy, particles with the light speed correspond to product states, stationary particles maximally entangled states, and particles slower than light partially entangled states. Furthermore, by quantifying the amount of entanglement with concurrence, we can show an intriguing relation between the concurrence E and the particle’s speed v [1],
![]()
- [1] F. Morikoshi, Prog. Theor. Exp. Phys. 123A04 (2015).
|
| Fig. 1. Correspondence between world lines and entanglement in a light cone (2+1 dimensions). |