Finite-key Security Analysis of Quantum Key Distribution withImperfect Light Sources
Sending confidential information such as a password over a communication channel needs to be encrypted. Among the many encryption methods, the one-time pad is the only encryption scheme rigorously proven to be secure. This crypt requires a key, which is a random bit string, and if its information is kept from an eavesdropper the one-time pad is secure. Therefore, secure distribution of the key is critical, and so key distribution (QKD) has attracted much attention as a means to accomplish this. For the secure distribution, a QKD system has to satisfy requirements imposed by a security proof. Unfortunately, most of the requirements in existing security proofs are hard to meet in practice. Therefore, to guarantee the implementation security, that is the security of a real-life QKD system, we need to construct security proofs with relaxed requirements.
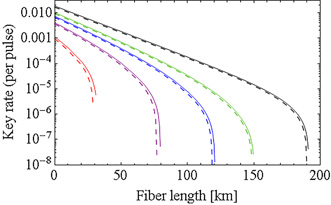
In previous work [1], we modified the security proofs to accommodate the effect of imperfect phase modulation (PM) in the asymptotic limit of a large number of the pulses. In this current work, we have generalized it to the one with a finite number of pulses [2]. Figure 1 shows one of our results where the horizontal (vertical) axes represents the fiber distance (the secret key generated per pulse). The solid (dashed) lines correspond to the case of the perfect (imperfect of 8.42°) PM. Moreover, the colors represent the number of pulses, and each line, form right to left, corresponds to the asymptotic limit, 1012, 1011, 1010, 109, respectively. The small differences between the solid and dashed lines mean that the effect of the imperfect PM is negligible. As the clock rate of most of the QKD system is more than 1 GHz, our results show the feasibility of secure key distribution with current QKD systems. These results constitute an important step towards guaranteeing implementation security for QKD systems.
Our work is in part supported by NICT.
- [1] K. Tamaki et al., Phys. Rev. A 90, 052314 (2014).
- [2] A. Mizutani et al., New J. Phys. 17, 093011 (2015).
|
| Fig. 1. Communication distance vs Key generation rate per pulse. |