Simulating the Spin Ising Model with Phonons
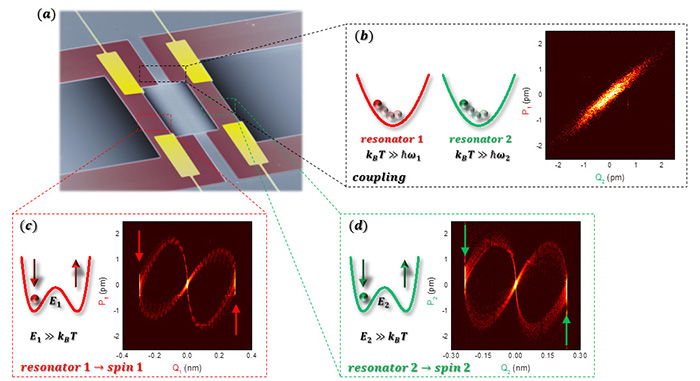
Physical simulators, composed of atoms, ions, photons or electrons, have emerged as a novel means for solving intractable mathematical problems [1]. Here this concept is extended to phonons that are localised in spectrally pure resonances in an electromechanical system [Fig. 1(a)] which enables their interactions to be exquisitely fashioned via piezoelectricity [2]. Specifically the electromechanical system is developed to mimic the spin Ising Hamiltonian where its spin 1/2 particles are replicated by the phase bi-stable vibration from a mechanical parametric resonance where multiple resonances play the role of a spin bath [Figs. 1(c),(d)]. The coupling between the mechanical spins is created via non-degenerate parametric down-conversion which entwines the resonances resulting in correlated vibrations [Fig. 1(b)]. The combination of parametric resonance and parametric down-conversion can then be harnessed to imitate a ferromagnetic, random or an anti-ferromagnetic state on-demand, whose statistical dynamics are consistent with the idealized spin Ising interaction. These results suggest that the electromechanical system could be further developed to imitate the spin Ising model in a non-trivial configuration, namely with a large number of spins with multiple degrees of coupling, a task that would overwhelm a conventional computer [3].
This work was supported by MEXT KAKENHI JP15H05869.
- [1] I. Buluta and F. Nori, Science 326, 108 (2009).
- [2] I. Mahboob et al., New J. Phys. 18, 083009 (2016).
- [3] I. Mahboob et al., Sci. Adv. 2, e1600236 (2016).
|
| Fig. 1. (a) A false colour scanning electron micrograph of the electromechanical system. Each mechanical resonator (1 and 2) has a vibration in its position which can be decomposed into in-phase (Q) and quadrature (P) components. (b) The vibration of the resonators, with frequency ω, can be visualised as balls rolling in harmonic potentials driven by thermal energy kBT. The parametric down-conversion correlates the vibration of the two resonators, effectively coupling them, which is confirmed via a linear inter-dependence of the in-phase and quadrature components of the two resonator’s motion. (c) and (d) Parametric resonance is manifested as either resonator having two large amplitude vibrations, with opposite phases, in phase-space and an off thermal state at the origin. This behaviour corresponds to the underlying harmonic potential of the resonators evolving into a double well potential, with barrier energy E being greater than kBT thus enabling spin information to be encoded. |