Koji Muraki, Tadashi Saku, and Yoshiro Hirayama
Physical Science Laboratory
The quantum Hall (QH) effect in a two-dimensional electron gas (2DEG) subjected to a strong magnetic field at low temperatures is an outstanding example of quantum phenomena that appears in macroscopic systems. The electronic state for each Landau-level filling in a single-layer 2DEG is unique to the material parameters such as the effective mass. However, when two layers of 2DEGs are separated by a distance of 10-20 nm in a double-quantum-well structure, the new internal degree of freedom associated with the layer in which the electrons reside leads to various electronic states, from which one can expect novel physical properties to emerge. Furthermore, such a system is interesting in that one can control the interlayer tunneling and Coulomb interactions by designing the heterostructure appropriately.
We have succeeded in fabricating a bilayer electron system with arbitrarily tunable densities using a double-quantum-well structure in which the field effect of the back gate is used in conjunction with modulation doping [1]. Using this structure, we elucidate electronic states specific to bilayer systems by applying an electric field perpendicular to the layers. Figure 1 shows the behavior of the magnetoresistance when the electron densities of the two layers are varied independently. The dark regions represent the QH effect. The dashed line shows the balance point where the electron densities in the two layers are equal. As the electrons are transferred from one layer to another by the electric field (shown by the arrow in the figure), we observe various characteristics of the QH states. Some of the QH states are destroyed by the electric field, while others continue to exist. We explain these observations in terms of level splitting and crossing due to the electric field (Fig. 2) [2]. According to this model, the effect of the electric field can be understood by analogy to the effect of a magnetic field on atoms or molecules (the Zeeman effect). (This work has been done in collaboration with the group of Profs. Ezawa and Sawada, Tohoku University.)
[1] K. Muraki et al., Jpn. J. Appl. Phys. 39 (2000) 2444.
[2] K. Muraki et al., Solid State Commun. 112 (1999) 625.
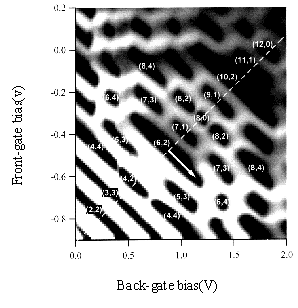
Fig. 1. Gray-scale plot of longitudinal resistance in a constant magnetic field.
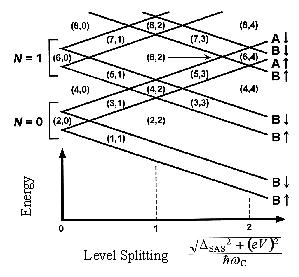
Fig. 2. Energy levels in bilayer systems vs. level splitting due to tunneling and electric field.
Back