Kaoru Shimizu and Akira Kawaguchi*
Optical Science Laboratory
Quantum behaviors of a one-dimensional interacting spin system have attracted
many research interests because that offers some important theoretical
models for condensed matter physicist. Moreover, from the view of one-way
quantum computation, study of the spin system may provide a variable knowledge
for designing its operation scheme. In particular, it is most important
for us to establish a physically-clear interpretation for the variety of
the behaviors that are regulated by quantum uncertainty depending on the
different values of spin-spin interaction coefficient J
and external magnetic field h.
By adapting some knowledge of quantum entanglement to the one-dimensional
spin system, we here obtained an insight that the quantum behaviors of
the system can be characterized in a quantitative way by small numbers
of parameters; amplitudes and phases of four different types of quantum
correlation (four Bell-states) between neighboring two spins, though the
system is composed of many numbers of spins. We employed the one-dimensional
anti-ferromagnetic Ising spin model represented by the Hamiltonian: H=J
S SZiSZi+1+h
xSSZi with the transverse magnetic field h
x. Then we studied
the behavior of pair-wise quantum entanglement† with
regarding the different values of h/J, where the system changes from the
random phase of SZj ( for
a large hx value) to the
ordered phase (anti-ferromagnetic phase for a small hx value). From critical behaviors of
the pair-wise entanglement observed around the phase transition point, we can conclude
that the amplitudes and phases of different quantum correlation provide a
quantitative description of quantum spin fluctuation[1].
Our proposed method on the basis of the entanglement analysis is a useful
tool for understanding the quantum behaviors of one or two dimensional
spin systems.
[1] K. Shimizu and A. Kawaguchi, Phys. Lett. A 355 (2006) 176.
*Present address: Toyota Macs. Co. Ltd.
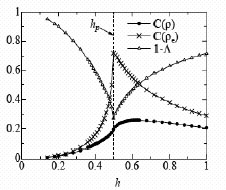
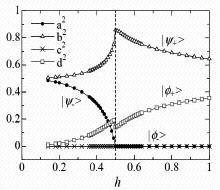
†Reduced density matrix r for the neighboring spins is decomposed into the separable part (1 -
L )rs and the inseparable part
Lre , (Fig.1) where
re is decomposed into the four Bell states so (Fig.2) that (1-
L) is minimal. We employ
concurrence C(r) as a quantitative measure of pair-wise entanglement.
 |
 |
|||||
|
|