![]()
![]()
(0) Question:
Can we define a proper refractive index of photonic crystals near the bandgap?
(1) Meaning of phase refractive index in periodic structures
Refractive index is generally meaningless in periodic structures ! (Fig. 1) (breakdown of Snell's law)
This is true for diffraction gratings and weakly-modulated photonic crystals.
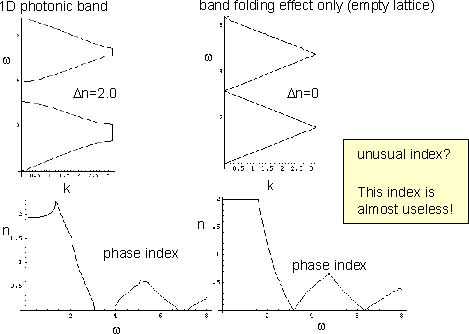
Fig.1: Phase refractive index calculated by textbook formula for 1D photonic crystal and 1D empty lattice. |
How about strongly-modulated photonic crystals?
(2) How about strongly-modulated photonic crystals?
Dispersion surface becomes rounded near the PBG (similar to Fermi surface in metals)(Fig. 2). Such dispersion surface resembles to that of homogeneous dielectric materials (Fig. 3).
Thus, Snell's law can be applied and effective refractive index can be defined.
However, the propagation direction can be negative because dw/dk can be negative in photonic crystals.
 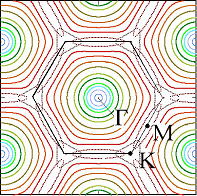 Fig. 2: dispersion surfaces of hexagonal PCs near the PBG |
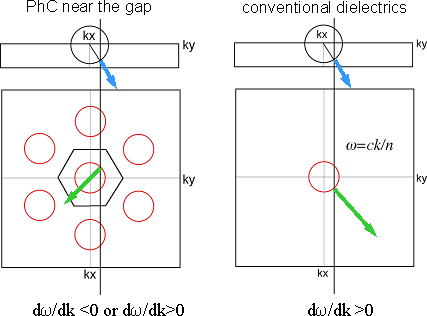 Fig. 3: dispersion surface plot for light incident.
|
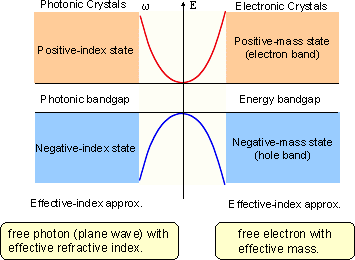
,(3) Effective index states in photonic crystals:
Analogy to effective-mass states in semiconductor
|
In the vicinity of the PBG, (1) Snell's law holds (2) Effective index can be defined. (3) Light propagation direction can be negative.
|
(4) Negative Refraction
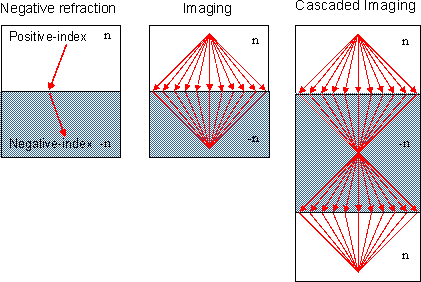 |
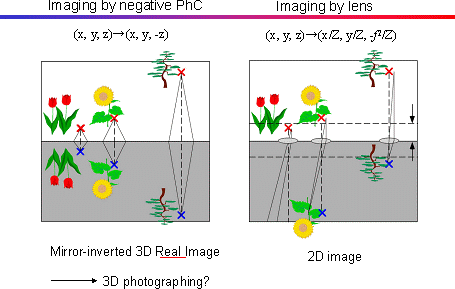 |
(5) Numerical Simulation of Negative Refraction
Finite-Difference Time-Domain (FDTD) simulation of light propagation in negatively-refractive photonic crystals.
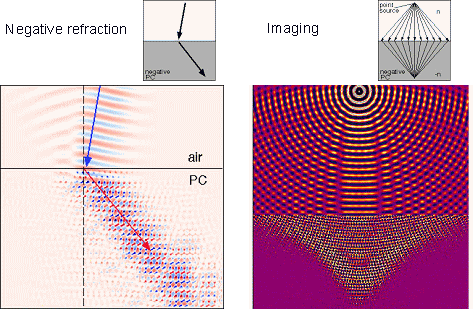 |