Research

Coherent Ising Machine


A coherent Ising machine (CIM) is a network of laser oscillators designed to find ground states of the Ising model based on the gminimum-loss principleh proposed by Y. Yamamoto and coworkers [1]. In a CIM, the problem, or spin-spin coupling terms of the Ising model are mapped onto the amplitude and phase of the optical couplings between the gartificial spinsh, represented by the phases of laser oscillators [1] or degenerate parametric oscillators (DOPO) [2,3]. By pumping the coupled oscillators slowly, the oscillator network tends to start oscillating at a phase configuration that minimize the total loss, that corresponds to the ground state of the Ising model represented by the oscillators.

In 2013, we started constructing time-multiplexed DOPOs using a long-distance (1 km) fiber cavity, where >2500 DOPOs were successfully obtained using dual-pump four-wave mixing in a nonlinear fiber as a phase sensitive amplifier (PSA) placed in a cavity [4]. This experiment was followed by the construction of DOPOs using a PPLN waveguide-based PSA [5], and further increase of the DOPO numbers to >10,000 [6,7]. These experiments paved a way towards a realization of a scalable CIM. Currently, the number of DOPOs generated by a single cavity increased to 50,000 with a phase stabilized cavity and >1 million with a free-run cavity [8]. In addition, we implemented one-dimensional Ising model using optically-coupled DOPOs, and confirmed that the networked DOPOs well simulated the behavior of low-temperature spins [7,9,10].

In 2016, we realized a 2048-node CIM based on the measurement-feedback scheme [11], where the spin-spin coupling are achieved by feedbacking the signal obtained from DOPO quadrature measurement to each DOPOs circulating in the cavity [12]. The CIM with the measurement-feedback scheme successfully found solutions to 2000-node maximum cut problems with less than a ten-thousandth of a second [11].

This research is financially supported by the ImPACT Program, where I serve as the Principal Investigator of the project named gCoherent Ising Machine based on large-scale time-multiplexed degenerate optical parametric oscillatorsh.

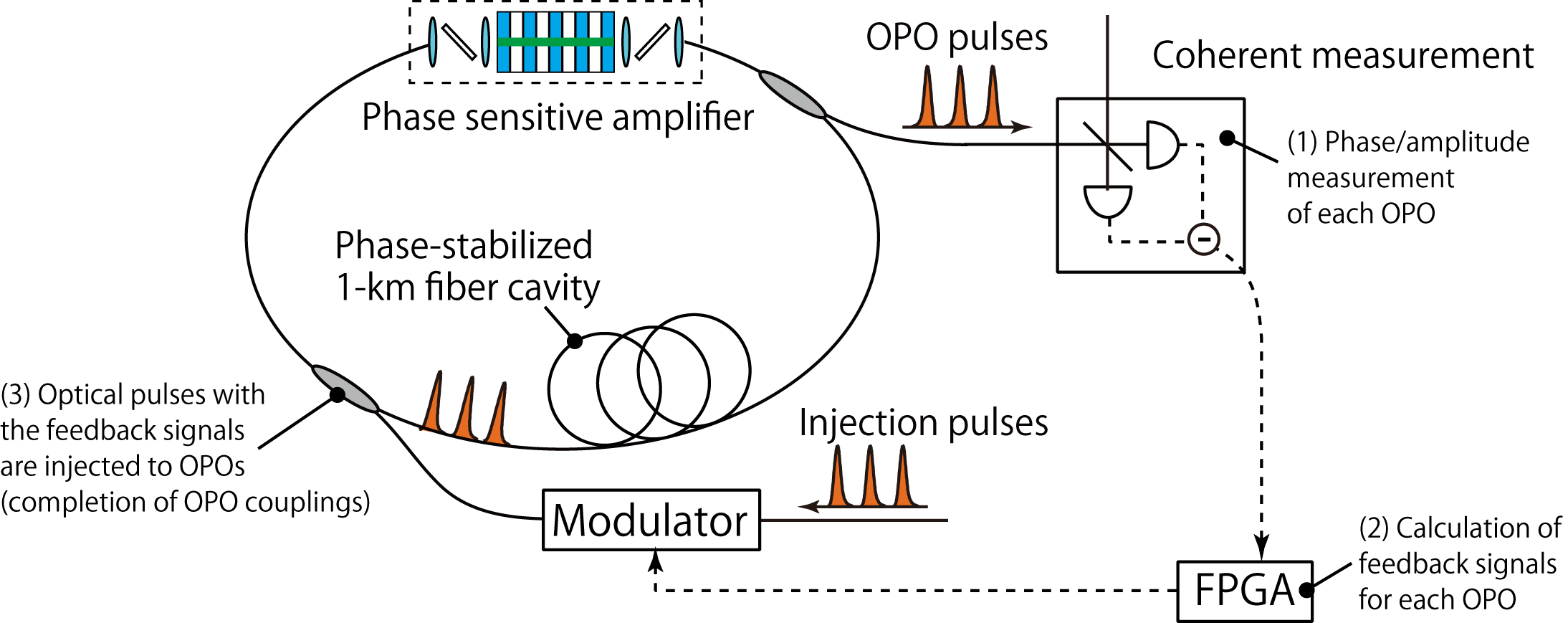
Fig: Coherent Ising machine with measurement-feedback.

  1. S. Utsunomiya, K. Takata, and Y. Yamamoto, gMapping of Ising models onto injection-locked laser systems,h Opt. Express 19, 18091 (2011).
  2. Z. Wang, A. Marandi, K. Wen, R. L. Byer, and Y. Yamamoto, gCoherent Ising machine based on degenerate optical parametric oscillators,h Phys. Rev. A 88, 063853 (2013).
  3. A. Marandi, Z. Wang, K. Takata, R. L. Byer, and Y. Yamamoto, gNetwork of time-multiplexed optical parametric oscillators as a coherent Ising machine,h Nature Photonics 8, 937 (2014).
  4. H. Takesue, T. Inagaki, K. Inoue, and Y. Yamamoto, "Coherence property of >2500-pulse multiplexed degenerate OPO," Japan Society of Applied Physics Spring Meeting 2014, 17p-PA1-1 (March 17, 2014).
  5. H. Takesue, T. Inagaki, T. umeki, O. Tadanaga, and H. Takenouchi,"Large-scale time-division multiplexed OPOs using PPLN waveguide," Japan Society of Applied Physics Spring Meeting 2015, 12a-P6-1 (March 12, 2015).
  6. H. Takesue, T. Inagaki, K. Inoue, and Y. Yamamoto, "Time-division-multiplexed degenerate optical parametric oscillator for a coherent Ising machine," IEEE Summer Topicals 2015, TuF4.2, July 14, 2015, Nassau, Bahamas (invited).
  7. T. Inagaki, K. Inaba, R. Hamerly, K. Inoue, Y. Yamamoto, and H. Takesue, "Large-scale Ising spin network based on degenerate optical parametric oscillators," Nature Photonics 10, 415-419 (2016).
  8. H. Takesue and T. Inagaki, "10 GHz clock time-multiplexed degenerate optical parametric oscillators for a photonic Ising spin network," Opt. Lett. 41, 4273-4276 (2016).
  9. T. Inagaki, K. Inoue, Y. Yamamoto, and H. Takesue, "Simulating one-dimensional Ising spins with optically-coupled timedivision-multiplexed optical parametric oscillators," Nonlinear Optics (NLO) 2015, NTu1B.6, July 28, 2015, Kauai, Hawaii.
  10. T. Inagaki, K. Inaba, H. Takesue, "Simulating 1-dimensional Ising model with an OPO network," Japan Society of Applied Physics Fall Meeting 2015, 15a-4D-3iSeptember 15, 2015j.
  11. T. Inagaki, Y. Haribara, K. Igarashi, T. Sonobe, S. Tamate, T. Honjo, A. Marandi, P. L. McMahon, T. Umeki, K. Enbutsu, O. Tadanaga, H. Takenouchi, K. Aihara, K. Kawarabayashi, K. Inoue, S. Utsunomiya, and H. Takesue, "A coherent Ising machine for 2000-node optimization problems," Science (2016)
  12. S. Utsunomiya, Y. Yamamoto, H. Takesue, PCT/JP2015/059057

Quantum Communication and integrated quantum photonics

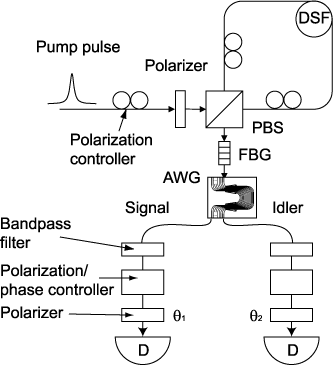
Fig.1: Configuration for generating polarization entanglement using spontaneous four-wave mixing (SFWM) in dispersion shifted fiber (DSF). H. Takesue and K. Inoue, Phys. Rev. A 70, 031802(R) (2004).

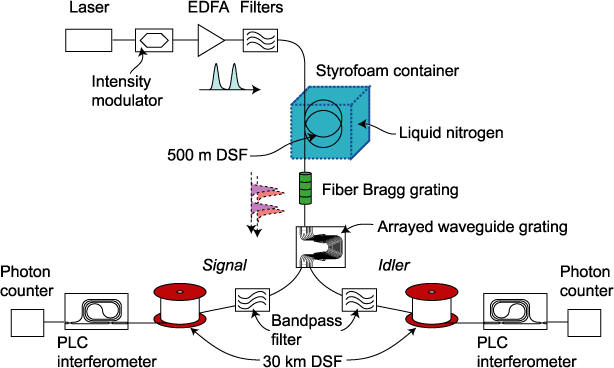
Fig.2: Configuration for generating time-bin entanglement using SFWM in cooled DSF. The DSF was cooled to suppress noise photons caused by spontaneous Raman scattering. H. Takesue and K. Inoue, Phys. Rev. A 72, 041804(R) (2005): H. Takesue and K. Inoue, Opt. Express, 13, 7832 (2005).

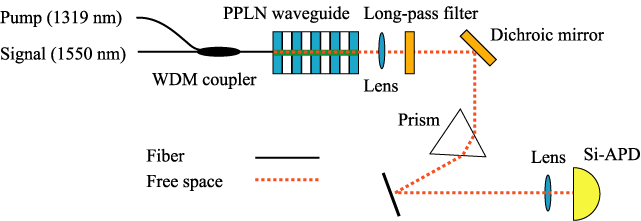
Fig.3: Frequency up-conversion single photon counter. C. Langrock et al., Opt. Lett., 30, 1725 (2005).

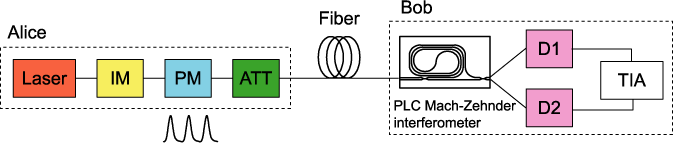
Fig.4: Configuration of differential phase shift quantum key distribution (DPS-QKD).

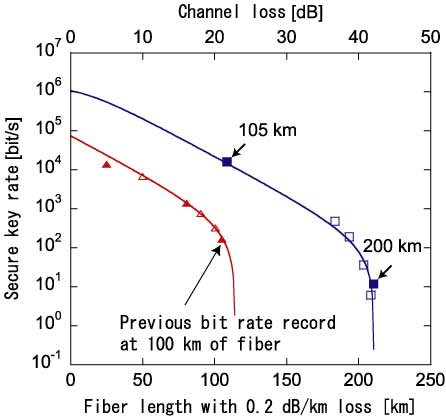
Fig.5: Experimental result of DPS-QKD: secure key generation rate as function of transmission fiber length. Secure keys with a bit rate of 12 bit/s was successfully generated over 200 km of fiber. H. Takesue et al., Nature Photonics 1, 343 (2007).

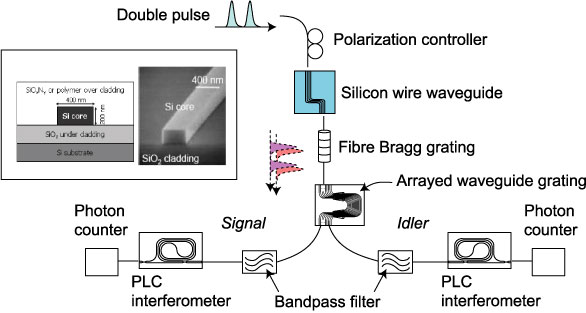
Fig.6: The setup of the first experimental entanglement generation using a silicon waveguide. Inset: the silicon wire waveguide used for the experiment fabricated by NTT Microsystem Integration Laboratories. H. Takesue et al., Appl. Phys. Lett. 91, 201108 (2007).

Wavelength-Division Multiplexing (WDM) Access Networks

Lightwave Frequency Synthesis and Its Applications

Home