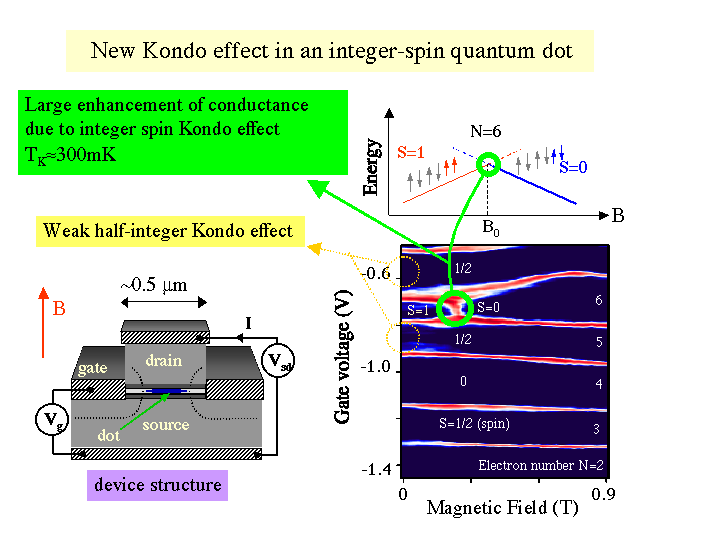
The Kondo effect is attracting renewed interest in mesoscopic physics decades after its discovery in bulk metals containing magnetic impurities. Recently, the Kondo effect has been observed in semiconductor quantum dots when a dot contains an odd number of electrons, or a half integer spin (S=1/2). Here, we report a novel Kondo effect, which appears when a dot contains an even number of electrons or an integer spin (S=0 and 1).
We study the Kondo effect in a vertical quantum dot where the number of
electrons (N) and their spin states (S) are clearly defined. The dot used in the present study is located in a rectangular mesa of 450 nm x 600 nm. We observe a spin triplet (S=1) at 0T for N=6. When a magnetic field is applied parallel to the current, a crossover to the spin singlet state (S=0) occurs, thus enabling us to tune the energy difference between the singlet and triplet states. At this transition, an anomalous increase in the N=6 valley conductance is observed between the 5th and 6th conductance peaks. A single peak at zero bias in the dI/dV vs V characteristic is observed when the gate voltage is fixed in the N=6 valley at the transition field, and the peak height increases logarithmically when the temperature decreases, exhibiting full Kondo behaviour. The Kondo temperature evaluated for the present case is much higher than for the ordinary S=1/2 case due to a multilevel effect.
Last updated on Jul. 7, 2000.
This page is maintained by S. Sasaki.

