Physical Science Laboratory
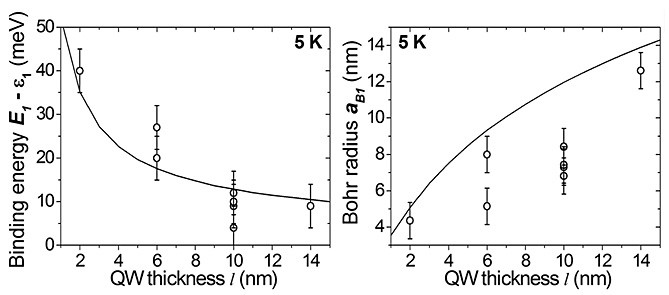
Impurities are fundamentally important for semiconductor device fabrication. In the simplest approximation, an impurity, or a point defect, inside a semiconductor is described as a hydrogen atom. The two essential properties of such impurity are the binding energy and the Bohr radius (aB1). Impurities in quantum wells (QWs) are affected by the confining potential if aB1 > l, where l is the QW thickness. (111)A-oriented, nominally undoped In0.53Ga0.47As surface QWs were grown by molecular beam epitaxy (MBE) [1]. We used the scanning tunneling microscope (STM) and the spectroscopy (STS) at the low-temperature (5 K) to study point defects behaving like donor impurities, which are natively located at the epitaxial surface of a QW. The electronic local density of states (LDOS) was measured with nanoscale resolution in the vicinity of single point defects. By measuring the LDOS in the QW, we are able to determine both the binding energy and the Bohr radius of single defects. Four different QW thicknesses were investigated in this work (l =2, 6, 10, and 14 nm). The obtained spatial dependence as the function of the distance r is well fitted by an exponential decay proportional to exp(-2r/aB1), representing the 1s hydrogenic wave function. Figure 1 summarizes the STS data obtained in this work. The smaller l, the larger binding energy E1-ε1, and the smaller aB1, i.e. the tighter the electron is bound to the point defect. Here, E1 is the bottom of the two-dimensional subband of the QW, and ε1 is the ground level of the impurity bound states. We clearly observe the influence of quantum confinement on the bound states, as expected in the case aB1 > l. If STS data are compared with a calculation of hydrogenic impurity states, the binding energy and the Bohr radius were found to be functions of the quantum well thickness, in quantitative agreement with variational calculations of hydrogenic impurity states [2]. It is remarkable that this calculation requires no adjustable parameter. The increase of E1-ε1 (or, equivalently, the decrease of aB1) with decreasing l is enhanced by the conduction band nonparabolicity.
[1] S. Perraud, K. Kanisawa, Z.-Z. Wang, and T. Fujisawa, Phys. Rev. B
76 (2007) 195333.
[2] G. Bastard, Phys. Rev. B 24 (1981) 4714.
 |
||
|