Single-Shot Readout of a Josephson Persistent Current Quantum Bit

Single-Shot Readout of a Josephson Persistent Current Quantum Bit
　
Kouichi Semba, Hirotaka Tanaka, Shiro Saito, and Hayato Nakano
Physical Science Laboratory
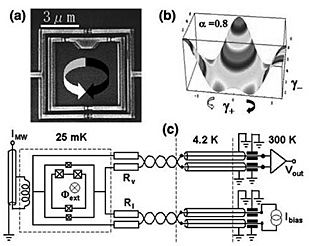
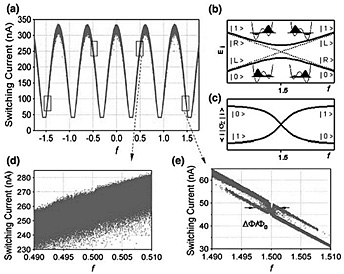
　In order to measure the quantum state of a persistent current quantum bit (a flux qubit), we use a dc-SQUID as a detector [1]. By carefully designing the junction parameters, the inner loop of Fig. 1(a) can be made to behave as an effective quantum two-state system, qubit. The qubit is described by the Hamiltonian H_q=(ε_f σ_z+Δσ_x)/2, where σ_x,z are the Pauli matrices. Due to the fluxoid quantization, the two eigenstates of σ_z are almost localized states with the supercurrent circulating in opposite directions, i.e., the clockwise state |R> and the counter-clockwise state |L>. The dc-SQUID picks up a signal that is proportional to σ_z . Figure 2(a) shows the modulation of the measured dc-SQUID switching current against the external magnetic flux as a function of f =Φ_ext/Φ₀, where Φ₀ is a flux quantum h/2e. Each dot in the graph corresponds to every single readout without averaging. The classically stable current eigenstates |L> and |R> are no longer stable in the presence of quantum tunneling Δ. As shown in Fig. 2(b), qubit energy eigenstates |0> and |1> are superpositions of macroscopically distinct states |L> and |R>. In Fig. 2(e) near f =1.5, where Δ>>ε_f ～0 and the switching current distribution is sharp enough to observe the χ -shaped qubit step clearly. The thicker stripe corresponds to the ground state |0> and the other stripe corresponds to the excited state |1>. These facts clearly show that we can carry out a single-shot σ_z projection measurement to |L> or |R> with the aid of a Φ_ext shift pulse, in the same way as the Stern-Gerlach apparatus for measuring a superposed spin-state. The merit of our dc-SQUID readout is that we can control interaction strength between the qubit and the detector dc-SQUID, at will. In the Stern-Gerlach case, it was always fixed and was definitely larger than energy difference of the spin eigenstates. This gives us a possibility of realtime control of the quantum readout itself.
[1] K. Semba et al., Quantum Information Processing 8 (2009) 199.

　

Fig. 1. (a) Scanning electron micrograph of a superconducting qubit (inside loop) and a dc-SQUID (outside loop) as a detector. A pair of arrows indicate distinct supercurrent states |L> and |R> of the qubit. (b) The potential energy of the qubit in phase space. (c) Schematic diagram of the measurement setup. Qubit was measured at dilution temperature of 25 mK.

Fig. 2. (a) Switching current of the dc-SQUID detector.
f =Φ_ext/Φ₀, where Φ_ext is the external magnetic flux penetrating the qubit loop. (b) Schematics of the qubit energy eigenstates{ |0>, |1>} and current eigenstates { |L>, |R>}. (c) Expected readout for states{ |0>, |1>}. (d) Zoom in near f =0.5. (e) Zoom in near f =1.5. Qubit states |0> and |1> can be readout distinctly.

[back]　[Top]　[Next]