Optomechanics Using Excitonic Transitions in Semiconductor Heterostructures

Hajime Okamoto¹, Takayuki Watanabe^1,2, Ryuichi Ohta¹, Koji Onomitsu³,
Hideki Gotoh⁴, Tetsuomi Sogawa⁴, and Hiroshi Yamaguchi^1,2
¹Physical Science Laboratory,²Tohoku University, ³Materials Science Laboratory,
⁴Optical Science Laboratory

　Optical control of micromechanical resonators has been widely demonstrated via cavity-enhanced radiation pressure or photothermal backaction [1]. Such cavity optomechanics allow highly tunable manipulation of a single mechanical resonator, including vibration amplification and damping (i.e., mode cooling). However, it cannot be straightforwardly extended to integrated mechanical systems because it needs delicate cavity operation, including tapered-fiber access and coupling adjustment. Thus, an alternative cavity-free approach is highly demanded in order to practically apply the optical control capability to integrated micromechanical systems. Here, we present excitonic optomechanics implemented in a compound semiconductor microcantilever. By using opto-piezoelectric stress induced via excitonic transitions, cavity-free control of a micromechanical resonator is achieved [2].
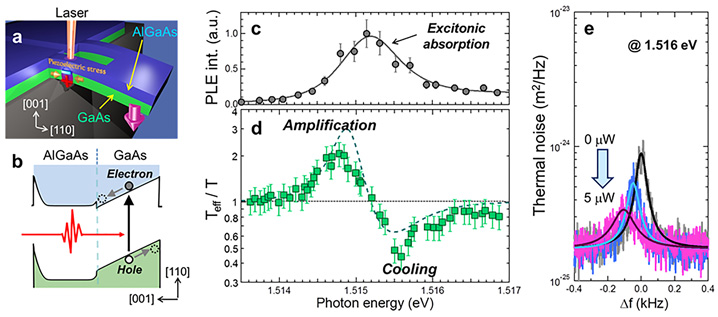
　We used the AlGaAs/GaAs heterostructured cantilever shown in Fig. 1(a). In this system, the optically excited electrons and holes are separated via the built-in electric field [Fig. 1(b)]. This causes piezoelectric (compressive) stress along the longitudinal direction in the GaAs layer, which leads to downward bending of the cantilever [Fig. 1(a)]. This effect depends on the optical absorption and on strain via the deformation potential. Therefore, strain-dependent opto-piezoelectric stress appears around the exciton resonance, where the per-strain change in the optical absorption is maximized. Since this stress acts on the cantilever in a time delay with respect to the optical excitation, it causes a self-feedback effect on the mechanical vibration, where the sign and gain of the self-feedback depend on the slope of the absorption spectrum [Fig. 1(c)]. We achieved both vibration amplification and mode cooling (damping) by detuning the photon energy from the exciton resonance [Fig. 1(d), (e)].