Optical Control of Mechanical Mode Coupling at Room Temperature

Ryuichi Ohta¹, Hajime Okamoto¹, Rudolf Hey²,
Klaus-Juergen Friedland², and Hiroshi Yamaguchi¹
¹Physical Science Laboratory, ²Paul-Drude-Institut für Festkörperelektronik

　The ability to manipulate mechanical vibrations and their transportation in multiple mechanical modes are of great interest for practical applications of mechanical systems, such as to mechanical logic circuits and acoustic metamaterials. For this purpose, tunable intermodal coupling, which is induced by the modulation of tension at the modes’ frequency difference, is highly desired at room temperature. If the coupling rates of different mechanical modes exceed the damping rate of each mode, called the strong coupling regime, we can quickly transfer the vibrations from one mode to another and thereby achieve fast switching of mechanical resonators [1]. Such a demonstration has so far been reported in GaAs mechanical resonators at cryogenic temperatures using piezoelectric stress modulation. However, it is difficult to extend it to room temperature, because the coupling rate achieved by the piezoelectric effect is too small to overcome the mechanical damping rate at room temperature. In this work, we demonstrate strong and tunable coupling of two mechanical modes at room temperature by using laser-induced photothermal stress modulation [2].
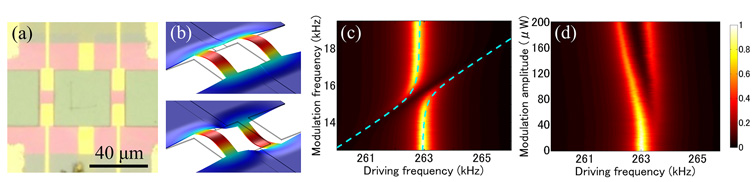
　Figure 1(a) shows a microscope image of two mechanical resonators connected to each other. Figure 1(b) shows symmetric and anti-symmetric modes calculated by the finite element method. These resonators were fabricated on a GaAs wafer containing AlAs/GaAs superlattices. Applying a laser whose wavelength is 780 nm causes photothermal expansion in the GaAs layer, which provides the internal stress in a mechanical resonator. The internal stress generates the coupling of the symmetric and anti-symmetric modes, when the laser is modulated to the difference frequency of the two modes. Figure 1(c) shows the mechanical spectrum of the anti-symmetric mode at various frequencies of the amplitude-modulated laser, and Fig. 1(d) shows the modulation-amplitude dependence of the spectrum. When the modulation frequency is close to the differential frequencies of the two modes, we can clearly observe the mode splitting, where the amount of the split corresponds to the coupling rate. As shown in Fig. 1(d), the coupling rate can be controlled by changing the modulation amplitude. The maximum coupling rate is 2.57 kHz. It exceeds the damping rates of both modes at room temperature (2.14 and 1.59 kHz), which indicates that the strong coupling of two mechanical modes is achieved at room temperature.
　This work was supported by KAKENHI.