Observation of Quantum Zeno Effect in Superconducting Flux Qubit
It is known that an ideal quantum measurement stochastically projects a quantum state into an energy eigenstate. As the distance between the target state and eigenstate becomes smaller, the probability of projecting it into the eigenstate increases. If the quantum state is modified even slightly from the initial eigenstate due to a time evolution, the probability of projecting it into the eigenstate approaches unity. This means that frequent quantum measurements can freeze a specific time evolution of a quantum system where the holding time of the state depends on the measurement period. This phenomenon is both academically interesting and useful for many applications such as the estimation of quantum measurements and the realization of a decoherence free subspace.
A superconducting flux qubit is composed of a superconducting loop circuit with Josephson junctions. By applying a characteristic bias field, we can manipulate this circuit as a quantum two-level system with an energy of several GHz. We implement Rabi oscillations by applying a resonant microwave to the superconducting qubit, and attempt to freeze the Rabi oscillations by applying periodic measurement pulses. To induce the projection, we use a Josephson bifurcation readout, which is a quantum non-demolition measurement.
Fig. 1 (a) shows the probability of detecting excited flux qubit in the time domain with a resonant microwave pulse. Without projections, we can clearly observe Rabi oscillations between the excited and ground states. On the other hand, with the projections, the Rabi oscillation is suppressed, and the qubit remains in the excited state. Fig. 1 (b) shows the probability of detecting excited flux qubit when we change the measurement period. As the measurement period decreases, the holding time increases. These results are well explained by a model of the quantum Zeno effect. This is the first demonstration to observe the quantum Zeno effect on a superconducting qubit by using periodic quantum measurements [1].
- [1] K. Kakuyanagi et al., New J. Phys. 17, 063035 (2015).
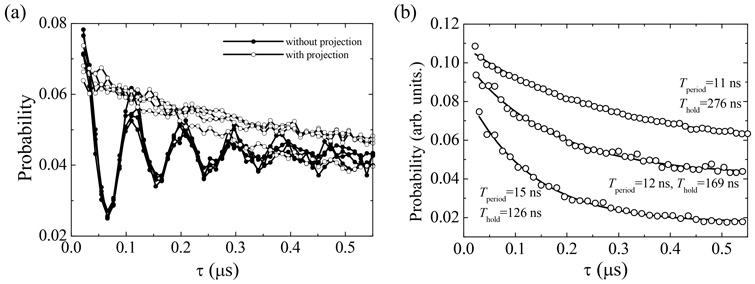
|
| Fig. 1. (a) Time evolution of qubit with and without measurement pulse. (b) Holding time of quantum state with different measurement periods. |