Coherent Ising Machine for Combinatorial Optimization Problems

Takahiro Inagaki, Kensuke Inaba, Toshimori Honjo, and Hiroki Takesue
Optical Science Laboratory

　It is known that combinatorial optimization problems can be mapped onto ground-state-search problems of the Ising model. Recently, several approaches have been demonstrated to solve the Ising problems using artificial spin systems. A coherent Ising machine (CIM) can simulate the Ising model with networked degenerate optical parametric oscillators (DOPOs). A DOPO takes only a 0 or π phase relative to the pump pulse, so this binary phase mode can represent the binary spin state of the Ising model. To solve complex problems with the CIM, we need to prepare a large number of DOPOs and connect them with each other through mutual optical couplings. We generated over 10,000 DOPOs via time-domain multiplexing in a 1-km fiber ring cavity [1,2]. Using those DOPOs, a one-dimensional Ising model was simulated by introducing nearest-neighbor optical coupling with a 1-bit delay interferometer. We observed the ferromagnetic and anti-ferromagnetic behavior of low-temperature Ising spins with the networked DOPOs.
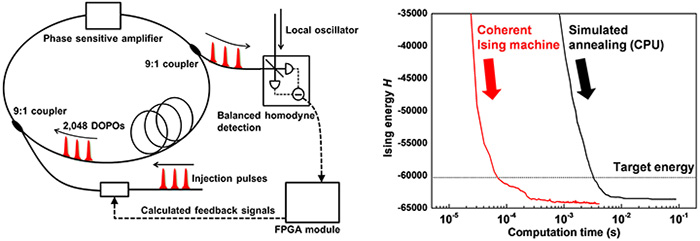
　To implement all-to-all optical couplings among DOPOs, we employed a measurement and feedback (MFB) scheme [Fig. 1 (left)]. A portion of the DOPOs are measured using a balanced homodyne detector. The measured signals are then input into a field-programmable gate array (FPGA) module, where a feedback signal for each DOPO is calculated according to the network structure. The calculated feedback signals are converted into optical pulses, and launched into the cavity to achieve the virtual optical couplings between DOPOs. With the MFB scheme, we developed a CIM that could find solutions to optimization problems on arbitrary graph structures with up to 2,048 nodes [3]. We performed a benchmark study to investigate the performance of our CIM to solve an optimization problem and compared it with a simulated annealing (SA) algorithm. We used the CIM and SA to solve the maximum-cut (MAX-CUT) problem for a 2,000-node complete graph with 1,999,000 undirected edges. The times needed to reach the target Ising energy were about 70 μs for the CIM and 3.2 ms for SA [Fig. 1, (right)]. The CIM obtained the benchmark Ising energy nearly 50 times faster than SA. These results suggest that a CIM can outperform SA on a CPU when solving dense graph problems.
　This work was supported by the ImPACT Program.