Quantum State Tomography for High-dimensional Time-bin States
High-dimensional quantum states are being investigated as resources of advanced quantum information processing. Because a high-dimensional state has multiple orthogonal states, for example, we can increase the information that a particle can carry (multiple bits per particle). A time-bin state is often used in photonic quantum communication systems because a time bin state is robust against disturbances caused by optical fiber transmission. Furthermore, we can easily enlarge the number of dimensions of the state simply by increasing the number of time slots that form it. To evaluate the quality of the state, it is important to fully characterize the quantum state via quantum state tomography [1,2]. However, a method of quantum state tomography for high-dimensional time-bin states was not known prior to our research. Here, we demonstrated a quantum state tomography scheme for high-dimensional time-bin states using cascaded Mach-Zehnder interferometers [3]. With this scheme, the number of the measurement settings scales linearly with the dimension of the state [3].
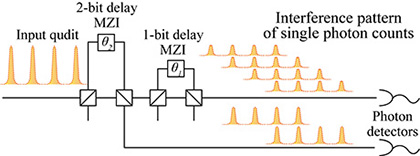
Figure 1 shows the concept of quantum state tomography using cascaded Mach-Zehnder interferometers. The information of a high-dimensional time-bin state is encoded at multiple temporal positions and in the relative phases between the positions. After a photon passes through the cascaded Mach-Zehnder interferometers, it makes an interference pattern of single photon counts depending on its state and the settings of the interferometers. By observing the interference pattern while changing the settings of the interferometers, we can obtain information on the temporal positions and relative phases encoded in the photon and reconstruct the state with that information.
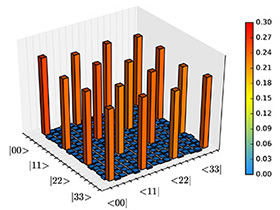
We performed quantum state tomography on four-dimensional time-bin entangled states generated via spontaneous parametric down-conversion in a periodically poled lithium niobate waveguide. We obtained a reconstructed state that was close to the four-dimensional maximally entangled time-bin state (Fig. 2). The number of measurement settings was 16, which was equal to the dimension of the Hilbert space for the two entangled photons. Thus, we successfully demonstrated an efficient quantum state tomography for high-dimensional time-bin states.
- [1] D. F. V. James et al., Phys. Rev. A 64, 052312 (2001).
- [2] R. T. Thew et al., Phys. Rev. A 66, 012303 (2002).
- [3] T. Ikuta and H. Takesue, New J. Phys. 19, 013039 (2017).
|
|
| Fig. 1. Concept of the quantum state tomography using cascaded Mach-Zehnder interferometers. | Fig. 2. Real parts of the reconstructed four-dimensional maximally entangled state. |