Fundamental Rate-loss Trade-off for the Quantum Internet
The quantum internet holds promise for accomplishing many quantum communication tasks
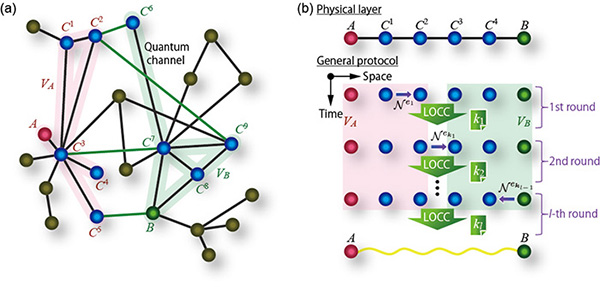
—such as quantum teleportation and quantum key distribution (QKD)—freely between any clients all over the globe, as well as the simulation of the evolution of quantum many-body systems. The most primitive function of the quantum internet is to provide quantum entanglement or a secret key (for secure communication) to two points in the network [such as A and B in Fig. 1(a)] efficiently.
In our work, we present a general theoretical limit on the performance of such quantum internet protocols [Fig. 1(b)], determined only by the properties of communication channels in the network [1]. This theoretical limit is obtained by generalizing the Takeoka-Guha-Wilde (TGW) bound [2] which upper bounds the private/quantum capacities of single communication channels. Therefore, our theoretical limit inherits a feature of the TGW bound that it can be estimated for any communication channel, and our limit can thus be estimated irrespectively of what kind of communication channel constructs the quantum network. In fact, for any quantum communication protocol working over linear networks composed of optical fibres, this feature enables us to derive a trade-off relation between the communication rate and the loss in the network. This trade-off has essentially no scaling gap with the quantum communication efficiencies of known protocols such as intercity QKD protocols and quantum repeater protocols. In other words, this implies that there remains not much room to improve known intercity QKD protocols and quantum repeater protocols with respect to the efficiency. As another example of applications of our theoretical limit, we apply the limit to one of most famous quantum repeater schemes, called Duan-Lukin-Cirac-Zoller-type (DLCZ-type) schemes [3]. As a result, we conclude that the matter quantum memories in the DLCZ-type schemes should have coherence time (T2) larger than 0.1 ms at least, in order to enjoy the blessing of the DLCZ-type schemes. Our result—reveraling a practical but general limitation on the quantum internet—enables us to grasp the potential of the future quantum internet.
- [1] K. Azuma, A. Mizutani, and H.-K. Lo, Nature Commun. 7, 13523 (2016).
- [2] M. Takeoka, M. Guha, and M. M. Wilde, Nature Commun. 5, 5245 (2014).
- [3] N. Sangouard et al., Rev. Mod. Phys. 83, 33 (2011).
|
| Fig. 1. (a) Quantum network. (b) General quantum internet protocol. In the protocol, quantum channels, local operations and classical communication (LOCC) are freely combined. |