Kosuke Kakuyanagi, Shiro Saito, Hayato Nakano, and Kouichi Semba
Physical Science Laboratory
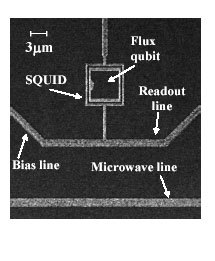
The superconducting flux qubit (Fig. 1) is a promising solid-based qubit that offers the advantage of scalability. We attempt to measure the magnetic field dependence of the phase relaxation time (T2) and energy relaxation time (T1) in order to clarify the decoherence of a superconducting flux qubit [1]. Relaxation is generally caused by the energy fluctuation that is generated from the interaction between qubits and their environment. Therefore, we can obtain information about the contribution of magnetic fluctuations to decoherence from field dependence measurements of the relaxations.
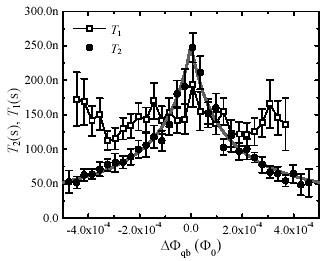
Figure. 2 shows measurement results for the magnetic field dependence of T1 and T2 near the degeneracy point (ΔΦqb=0). The magnetic field is plotted with flux quantum units (Φ0). The T2 values increase as the external magnetic field approaches the degeneracy point. At the degeneracy point, the T2 value reaches 250 ns. In contrast, theT1 values are uniform ( T1〜140 ns).
In general, T2 includes pure dephasing (
Energy relaxation is generated from high frequency fluctuations, whose frequency is the same as the qubit energy. These results suggest that the coherence time of a superconducting flux qubit improves when we suppress the high frequency noise. Next, we will attempt to improve the coherence time of the superconducting flux qubit.
[1] K. Kakuyanagi, et al., Phys. Rev. Lett. 98 (2007) 047004.
 |
 |
|||||
|
|