A challenge facing the development of quantum computers, which are expected to possess computational capabilities far exceeding those of conventional computers, is the correction of errors caused by environmental disturbances and/or inaccurate logic gate operations. By exploiting 'quasiparticles¹' that behave differently from fundamental particles in nature, a totally new architecture for quantum computation (topological quantum computation²) with exceedingly low error rate might be possible. Using a highly sensitive nuclear magnetic resonance3 technique, NTT and Japan Science and Technology Agency have unraveled the electronic state in a semiconductor device expected to host such exotic quasiparticles. This achievement has been reported in the US science journal "Science" (published online January 26, 2012).

=> Quantum Solid State Physics Research Group

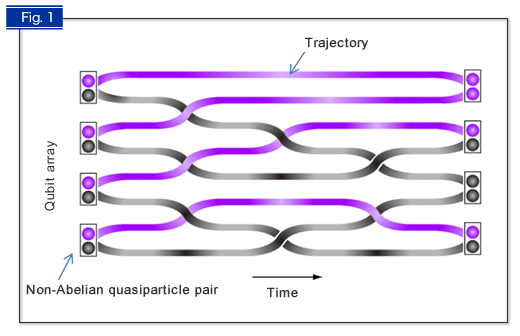
Fig. 1 Schematic illustration of topological quantum computation

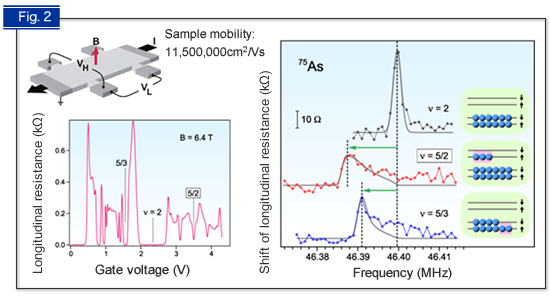
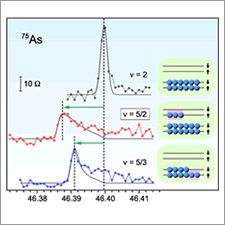
Fig. 2 Longitudinal resistance versus gate voltage (left) and nuclear magnetic resonance spectra for different electronic states (right).

A prime candidate for a system expected to host non-Abelian quasiparticles is the ν = 5/2 fractional quantum Hall state, an exotic electronic state that emerges in a pristine semiconductor heterostructure at very low temperatures and in high magnetic fields. (ν is the ratio between electron density and magnetic flux density, and is used to designate different electronic states.) The minimum in the longitudinal resistance labeled "5/2" signifies the emergence of this state. The shift of the peak frequency in the nuclear magnetic resonance spectra is proportional to the difference between the numbers of up- and down-spin electrons. By comparing spectra for different ν, we have demonstrated that the ν = 5/2 state is fully spin polarized. Our results serve to restrict the number of allowed theoretical models to only those supporting non-Abelian quasiparticles.

*1. Quasiparticle
Exchange of two fundamental particles such as electrons leaves the state indistinguishable from the original one. For quasiparticles—a group of many particles collectively behaving as if they were one, theory predicts those (non-Abelian quasiparticles) with exceedingly unusual properties; their exchange would transform the state into one distinct from the original.

*2. Topological quantum computation
A new method of quantum computation performed by rearranging non-Abelian quasiparticles. When there are 2n non-Abelian quasiparticles, the system has a degeneracy of 2ⁿ. Exchange of two quasiparticles takes the system from one of the 2ⁿ degenerate ground states to another, which is described as a unitary transformation and can thus be used as a quantum logic gate. The result of the calculation depends solely on the order of the quasiparticle exchanges and does not depend on the details of the quasiparticles' trajectories. This unique property of topological quantum computation is believed to make the error rate exceedingly low.

*3. Nuclear magnetic resonance (NMR)
Spectroscopic technique exploiting the resonant absorption of electromagnetic waves by nuclei placed in a strong magnetic field. Interactions of the nuclei with their environment shift their resonance frequency, which makes NMR a powerful means for structural and electronic analysis of matter.