First high-speed quantum-safe randomness generation with realistic devices
- An important advance towards the practical application of quantum randomness generation -
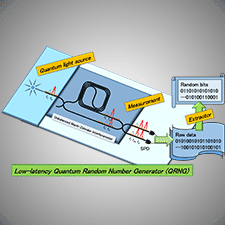
Researchers at the Nippon Telegraph and Telephone Corporation (NTT) have realized the first high-speed quantum random number generator (QRNG※1) that is built on realistic quantum devices. A QRNG is a quantum device that exploits the probabilistic nature of quantum measurements ※2 to generate genuine random numbers. These random numbers can be quantum-safe in the sense that their unpredictability can be certified even if an adversary correlates with the QRNG in a quantum manner. Previous high-performance QRNGs require fully characterized quantum devices. Therefore, they are subject to security loopholes when only realistic devices exist. Although there are QRNGs that are secure with realistic devices, they need to run for a long time to accumulate sufficient randomness ※3. This results in high latency from the initial request to the delivery of the requested random bits. It is desirable for real-world applications to realize QRNGs of low latency, high rate and high security. In this work, by developing an efficient method for certifying randomness (a collaborative work with the researchers at the National Institute of Standards and Technology) and by measuring the arrival time of an optical pulse with time-bin encoding ※4 we show that every 0.1 seconds a block of 8192 quantum-safe random bits can be generated, enabling low-latency high-rate performance. Further, our scheme guarantees the practical security with realistic quantum devices.
This work was published in the online-only journal Nature Communications on February 24, 2021.
=> Press Release
=> Quantum Optical State Control Research Group
Background
Random numbers are generated by a process or device termed the random number generator (RNG). The device output is a random number, if that output is unpredictable and uniformly distributed. The unpredictability promises that the output cannot be determined before running the device, while the uniformity ensures that the output will take each possible value with the same probability. Sometimes, we also require random numbers be private such that only the user of the RNG can learn their values. Random numbers are extremely useful in many scientific and real-world applications including numerical simulation, statistical sampling, gaming, and cryptography. One can obtain apparently-random numbers that exhibit some but not all the properties of random numbers via classical processes such as coin flips; however, any classical process is fundamentally deterministic ※3 and so cannot generate genuine random numbers. For this reason, we need to develop quantum random number generators (QRNGs).
Quantum mechanics offers many opportunities for generating genuine random numbers. For example, a genuine random bit can be generated by preparing a qubit ※5 in an equal superposition ※6 of its two basis states ※2 and then measuring it along that basis. Moreover, in contrast to classical processes, quantum processes generate certifiable random numbers based only on measurement observations with verifiable physical assumptions. Therefore, research efforts are going worldwide into realizing QRNGs. However, either the current QRNGs perform poorly (in terms of the rate achieved or the latency required for generating random numbers), or the assumptions underlying these QRNGs cannot be verified such that the practical security of the generated random numbers is not guaranteed. See Table 1 for detailed illustrations. For practical applications, it is important to devise a QRNG that performs well and at the same time ensures its practical security. This work reports such a QRNG for the first time.
Table 1. Comparison between different QRNGs.
Results
To illustrate the performance of their QRNG, the researchers consider a specific request for a block of 8192 quantum-safe random bits with a security error bounded by 2-64≈≈5.4×10-20. In the ideal case a QRNG will produce perfectly random bits that are distributed uniformly and uncorrelated with the adversary, while in practice the produced random bits can deviate from the perfectly random bits. The security error quantifies the maximum deviation of the actually produced bits from those produced in the ideal case, and it should be set at the request of random bits. The results presented in Figure 1 demonstrate that every 0.1 seconds the QRNG developed by the NTT can certify more than the number of requested random bit; the request is thus satisfied successfully. Further, this QRNG can be compared to other state-of-art QRNGs, as summarized in Table 1.
Technical points in detail
- A simple scheme using the photonic time-bin qubit
A photonic time-bin qubit is a stable qubit encoding information on the arrival time of a single photon ※7 and widely used for quantum communication. This qubit can be prepared in a basis state where the photon stays in a specific time position (top of figure 2) or a superposition state where the photon stays in both time positions simultaneously (bottom of figure 2). If we measure a photon prepared in a basis state onto the superposition state, the measurement result would be perfectly random in the ideal case. For a secure QRNG, we require not only the measurement on the superposition state but also the measurement on the basis state; the researchers used an unbalanced Mach-Zehnder interferometer ※8 and two single-photon detectors ※9 for these measurements, realizing a simple scheme of QRNG (figure 3). - Low latency and practical security by quantum probability estimation
The randomness in measurement results with respect to a quantum adversary is directly determined by the guessing probability (i.e., the maximum probability that the adversary can correctly guess the measurement results). The higher the guessing probability, the less the randomness in the measurement results is. Quantum probability estimation (QPE) is a theoretical method that estimates an upper bound on the guessing probability. This method requires a physical model of the QRNG considered. To ensure the practical security of the QRNG using realistic devices, the researchers included several imperfections in the light source and the measurement apparatus into the physical model appropriately. Furthermore, QPE can estimate the guessing probability more efficiently than other available methods, enabling low-latency QRNGs.
Outlook
The low-latency high-rate QRNG developed in this research is well suited for realizing a continuously-operating, high-security and high-speed quantum randomness beacon. A quantum randomness beacon is a server that repeatedly produces fixed blocks of fresh, certifiable, public random bits. These random bits have many applications such as for zero−knowledge proofs ※10 and election audits ※11. Another future development is to reduce the size of the developed QRNG such that it would become feasible to fabricate compact products. These would contribute to the realization of communication networks with high security enhanced by quantum technologies.
Publication Information
Title : A simple low-latency real-time certifiable quantum random number generator
Authors : Yanbao Zhang, Hsin-Pin Lo, Alan Mink, Takuya Ikuta, Toshimori Honjo, Hiroki Takesue, and William J. Munro
Journal : Nature Communications (2021), DOI: 10.1038/s41467-021-21069-8
Announce date : 24th February 2021, 10:00 London time (GMT)
Glossary
- ※1 ... A general quantum random number generator (QRNG)
- Illustrated in Figure 4 has three components: i) a source that can prepare the desired quantum states, ii) a measurement apparatus that can perform the desired measurements, and iii) an extractor that can extract the amount of certified randomness. The joint of the first and second components is realized by performing a quantum experiment, thus called the quantum process. On the other hand, the third component is realized by running a classical program, thus called the classical process.
- ※2 ... Quantum measurement
- A way of learning the state of a quantum system. The quantum state can be viewed as a vector in the state space (formally called the Hilbert space). According to the quantum superposition principle (which will be explained below), an arbitrary state can be decomposed as a sum of a few distinct states. These distinct states are called the basis states. Quantum measurement is the process of projecting a quantum state into these basis states. After the measurement, the quantum system will be in one of the basis states with probability determined by the overlap between the initial quantum state and the basis state. (Strictly speaking, the measurement described above is a projective measurement, and there are other types of quantum measurement.)
- ※3 ... Randomness
- An important concept and an essential resource in science, technology and real life. Roughly speaking, randomness expresses our lack of complete knowledge of the considered system, while a formal definition of randomness may vary depending on the field it concerns. Here we consider an operational definition that fits different purposes. We call an event random if the event cannot be correctly guessed in advance given our knowledge; otherwise, the event is deterministic.
- ※4 ... Time-bin encoding
- A technique used to encode a qubit (which will be explained below) on a superposition of two time slots (the early time bin and the late time bin). The time-bin encoding is robust against the loss of quantum information from a quantum system to its environment, and it can be prepared and measured in experiments by having a single photon going through an unbalanced Mach-Zehnder interferometer (which will be explained below).
- ※5 ... A qubit (or a quantum bit)
- A two-level quantum system, which is the basic unit of quantum information. For example, a qubit can be the spin of an electron where the two levels are spin up and spin down, or the polarization of a single photon where the two states are the vertical polarization and the horizontal polarization. In a classical system, a classical bit would have to be in one state or the other. However, quantum mechanics allows the qubit to be in a superposition (which will be explained below) of both states, a property which is fundamental to quantum mechanics and quantum information processing.
- ※6 ... Quantum superposition
- A fundamental principle of quantum mechanics. It tells us that, much like waves in classical physics, any two (or more) quantum states can be added together (or superposed) and the result will be a valid quantum state. Accordingly, a quantum system can be in two (or more) distinct quantum states simultaneously such that it is impossible to determine which quantum state the system takes before a measurement.
- ※7 ... A single photon
- The basic unit of light (strictly speaking, an elementary excitation of a single mode of the quantized electromagnetic field). An ideal single-photon source is a source that can emit a single photon at any time requested by the user.
- ※8 ... An unbalanced Mach-Zehnder interferometer (MZI)
- An optical instrument that can split a single beam into two and later combine the two beams together. We can observe constructive or destructive interference patterns depending on the difference between the optical path lengths transmitted by the two beams before they are combined. By using the interference, we can measure the time-bin qubit on superposition states.
- ※9 ... A single-photon detector
- A photodetector that can determine whether there is at least a single photon in the incoming optical signal or not. Single-photon detectors are useful in many fields including fiber-optic communication, quantum information science, astrophysics, and material science.
- ※10 ... A zero-knowledge proof
- A method by which one person can prove to another person that he/she knows a secret, without conveying any information apart from the fact that he/she knows the secret. The authentication systems in real life are examples of zero-knowledge proofs. For an authentication system, it is necessary to ensure that the user and the server can protect against any cheat on each other. For this purpose, public random bits are helpful.
- ※11 ... An election audit
- A process conducted after polls close for the purpose of determining whether the votes were counted accurately or whether proper procedures were followed, or both. To ensure the fairness and transparency, we need population samples selected randomly and in a way agreed by the public. Therefore, public random bits are needed.










