|
|
 |
 |
 |
 |
 |
 |
Home |
People |
Publications |
Positions |
Contact |
Link |
 Electromechanics |
Optomechanics |
Magnomechanics |
Nonlinear mechanics |
Phononic crystals and waveguides |
| Nonlinear mechanics |
| Recent Activities |
|
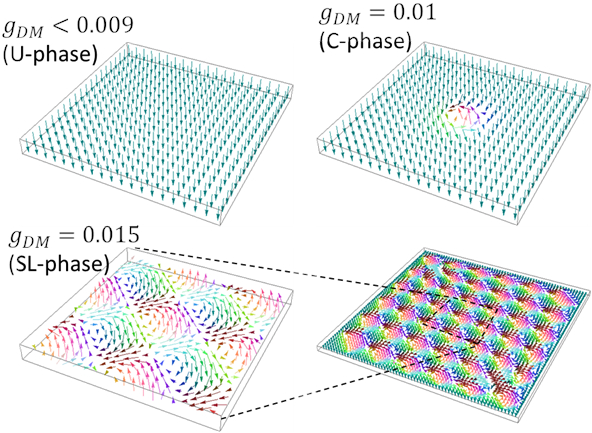
Quadrature skyrmions in two-dimensionally arrayed parametric resonators H. Yamaguchi, D. Hatanaka, and M. Asano, Phys. Rev. Research 5, 043076 (2023) |
| Skyrmions are topological solitons in two-dimensional systems and have been observed in various physical systems. Generating and controlling skyrmions in artificial resonator arrays lead to novel acoustic, photonic, and electric devices, but it is a challenge to implement a vector variable with the chiral exchange interaction. Here, we propose to use quadrature variables, where their parametric coupling enables skyrmions to be stabilized. A finite-element simulation indicates that an acoustic skyrmion would exist in a realistic structure consisting of a piezoelectric membrane array. |  |
|
Self-Sustained Libration Regime in Nonlinear Microelectromechanical Devices S. Houri, M. Asano, H. Okamoto, and H. Yamaguchi, Phys. Rev. Appl. 16, 064015 (2021) |
 |
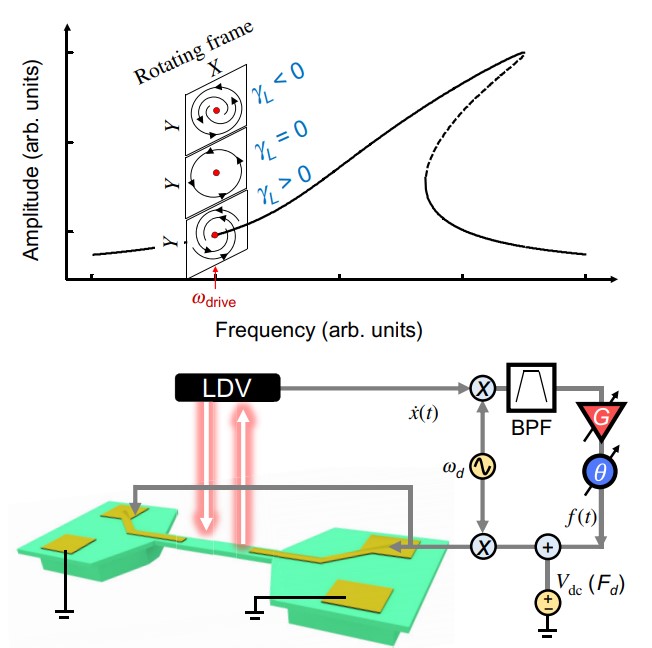We present a mode of operation for Duffing-type nonlinear microelectromechanical system devices whereby a self-sustained multifrequency output is generated. This self-sustained librator regime creates a limit cycle around a dynamical fixed point, i.e., around fixed points within the rotating frame, whereas a traditional oscillator generates a limit cycle around a static fixed point. The librator limit cycles thus created do not change the global topology of the rotating frame phase space, but are constrained by it. Because of the Duffing nonlinearity, different types of limit cycles could be generated within the same phase space, with each type possessing distinct dynamical features. Transitioning between these limit cycles requires crossing homoclinic bifurcations, which is done without generating chaos as the phase space dynamics are constrained in two dimensions. This work provides an alternative experimental tool for the study of microelectromechanical and nanoelectromechanical system dynamics and their application. |
|
Non-equilibrium quadratic measurement-feedback squeezing in a micromechanical resonator M. Asano, T. Aihara, T. Tsuchizawa, and H. Yamaguchi, Phys. Rev. Research 3, 033121 (2021) |
| Measurement and feedback control of thermomechanical motion in a micromechanical resonator has been actively studied to achieve extremely high sensing performance by controlling the stochastic thermal noise. Although linear measurement-feedback control in the phase space results in the feedback cooling, extending them to the nonlinear regime, i.e., utilizing quadratic of higher-order dynamic variables in both measurement and control, can further functionalize its operations. Here, we demonstrate fully quadratic measurement-feedback protocol in a micromechanical resonator by driving the second-order nonlinearity and directly measuring quadratic variables referred as Schwinger angular momentum. Our measurement-feedback protocol enables us to achieve a noise reduction at the level of -5.1 ± 0.2 dB over the -3-dB limitation in the continuous parametric driving. We unveil that this strong noise reduction originates in the effective cooling effect by investigating entropy production rates. These results would be further extended to investigating general performance of nonlinear information thermodynamic machines, in which the higher-order moments (e.g., variance and correlations) can be controlled with avoiding the nonlinear instability, thanks to the existence of information flows. |  |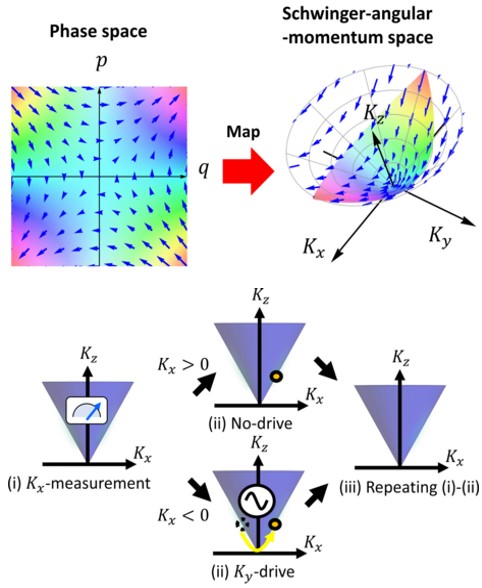
|
Generation and Propagation of Topological Solitons in a Chain of Coupled Parametric-Micromechanical-Resonator Arrays H. Yamaguchi and S. Houri, Phys. Rev. Applied 15, 034091 (2021) |
 |
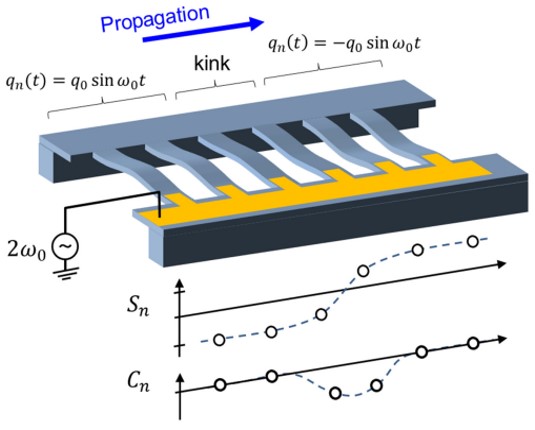Using a coupled parametric resonator array for generating and propagating a topological soliton in its rotating-frame phase space is theoretically and numerically investigated. In an analogy with the well-known ƒÓ4 model, the existence of a soliton is topologically protected, as the boundary of two different phase domains of parametric oscillation. Numerical simulation indicates that propagation can be triggered by switching of the phase state of one specific resonator, and the effects of damping, collision, and symmetry lifting by the harmonic drive on the propagation dynamics are studied. The topological soliton can be implemented by using electromechanical resonators, which allow its propagation dynamics to be precisely electrically controlled and provide a fully controlled on-chip test bed for the study of a topological soliton. |
|
Generic Rotating-Frame-Based Approach to Chaos Generation in Nonlinear Micro- and Nanoelectromechanical System Resonators S. Houri, M. Asano, H. Yamaguchi, N. Yoshimura, Y. Koike, and L. Minati, Phys. Rev. Lett. 125, 174301 (2020) |
| This Letter provides a low-power method for chaos generation that is generally applicable to nonlinear micro- and nanoelectromechanical systems (MNEMS) resonators. The approach taken is independent of the material, scale, design, and actuation of the device in question; it simply assumes a good quality factor and a Duffing type nonlinearity, features that are commonplace to MNEMS resonators. The approach models the rotating-frame dynamics to analytically constrain the parameter space required for chaos generation. By leveraging these common properties of MNEMS devices, a period-doubling route to chaos is generated using smaller forcing than typically reported in the literature. |  |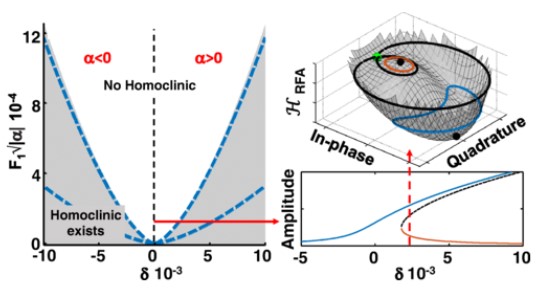
|
Demonstration of Multiple Internal Resonances in a Microelectromechanical Self-Sustained Oscillator S. Houri, D. Hatanaka, M. Asano, and H. Yamaguchi, Phys. Rev. Applied 13, 014049 (2020) |
 |
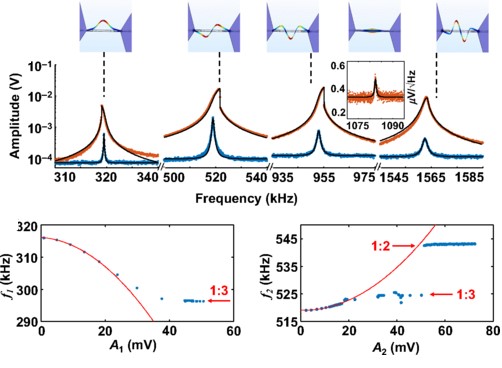We investigate the dynamics of a microelectromechanical self-sustained oscillator supporting multiple resonating and interacting modes. In particular, the interaction of the first four flexural modes along with the first torsional mode are studied, whereby 1:2, 1:3, and 2:1 internal resonances occur. Even and odd modes are induced to couple by breaking the longitudinal symmetry of the structure. Self-oscillations are induced in the second flexural mode via a gain-feedback loop; thereafter its frequency is pulled into a commensurate frequency ratio with the other modes, enabling the oscillator to act as a driver or pump for four modes simultaneously. |
|
Optically probing Schwinger angular momenta in a micromechanical resonator M. Asano, R. Ohta, T. Aihara, T. Tsuchizawa, H. Okamoto, and H. Yamguchi, Phys. Rev. A 100, 053801 (2019) |
| We report an observation of phononic Schwinger angular momenta, which fully represent two-mode states in a micromechanical resonator. This observation is based on simultaneous optical detection of the mechanical response at the sum and difference frequency of the two mechanical modes. A postselection process for the measured signals allows us to extract a component of phononic Schwinger angular momenta. This postselection scheme with the nonlinear measurement enables us to conditionally prepare two-mode states, which shows a noise reduction along a cross-phase quadrature and a finite correlation, from a randomly excited (uncorrelated) state. The phononic Schwinger angular momenta could be extended to high-dimensional symmetry [e.g., SU(N) group] for studying multipartite correlations in nonequilibrium dynamics with macroscopic objects. | 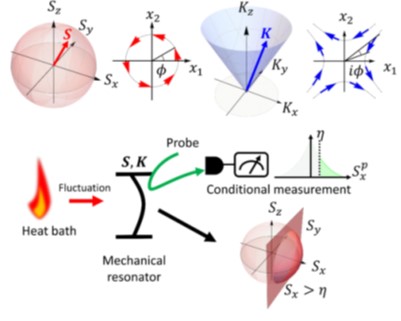 |