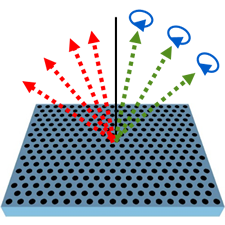
NTT物性科学基礎研究所（以下、NTT物性研）は、国立大学法人東京工業大学（以下、東工大）と共同で、誘電体周期構造を変形させるという簡単な手法により、光のトポロジカルな特異点を自在に生成・制御できる手法を、世界で初めて理論的に明らかにしました。本成果は、レーザの偏光状態や出射方向の制御に利用可能で、光のトポロジカルな性質を利用した新しい光制御の可能性を示すものと期待されます。

本成果は2020年7月31日（米国時間）に米国科学雑誌「フィジカル・レビュー・レターズ」のオンライン版に公開されました。

なお、本研究の一部は独立行政法人日本学術振興会科学研究費助成金の助成を受けて行われました。

⇒ニュースリリース
⇒フォトニックナノ構造研究グループ

研究の背景

トポロジーとは、物体に開いた穴の数のように、伸長や縮小などの連続変形では変わらない幾何学的な性質を扱う概念です。この性質は構造が持つトポロジカル数と呼ばれる数で規定され、穴の数はその一例です（図1）。この数で決定される性質があれば、形状の連続変形に影響を受けない強固な性質となります。この概念を固体中でバンド構造を組む電子に対して適用し、波数空間における電子の波動関数のトポロジーが様々な新しい物理現象を導くことを示した業績に対して2016年にノーベル物理学賞が与えられ、トポロジカル絶縁体を始めとする新しい物質相や新奇な物理現象が発見されています。最近になり、このトポロジカル物性は固体中の電子だけでなく、フォトニック結晶^*1と呼ばれる誘電体周期構造中の光においても発現することが判明し、光のトポロジカルな物性が次々に見つかっています。この分野はトポロジカルフォトニクス^*2と呼ばれ世界的に活発に研究されています。
　光のトポロジカルな現象の一つとして、光トポロジカル特異点と呼ばれるものがあります（図1）。これは光の偏光状態^*3が決めるトポロジカル数によって発現する状態で、特にトポロジカル数が整数の時にはBound state in the continuum (BIC)と呼ばれる特殊な状態が実現します（図2）。BICとは、本来閉じ込められないエネルギー領域にある波動が空間的に束縛されて閉じ込められる状態のことで、1929年からその存在が予言されていましたが、近年BICがフォトニック結晶中の光トポロジカル特異点として現れることが判っています。光のBICは、普通ならフォトニック結晶の外に光が漏れ出てしまうはずの周波数領域で、結晶の中に閉じ込められたモードとして出現します（図2）。
　フォトニック結晶において、面に垂直方向に光が出てこられない自明なBIC（垂直方向BIC）が存在することは以前より知られていましたが、最近になり斜め方向に光が出てこられない非自明なBIC（斜め方向BIC）が存在することがわかり、新奇な光閉じ込め方法として注目されています（図2下）。このBICモードに利得を与えるとレーザ発振が可能であり、閉じ込め方向にレーザ光が出射されることが知られています。これまでに、垂直方向の自明なBICを用いたレーザ発振が実現されています。また、斜め方向の非自明なBICでは斜め方向にレーザ発振可能であり、かつ発振する角度を変更可能であると考えられています。さらに、斜め方向のBICは、閉じ込めモードであるにもかかわらず面内に有限な群速度を持つなどの新奇な性質を持っており、広く興味を持たれて活発な研究が行われています。
　ところが、これまで発見された非自明な斜め方向BICは、ある構造条件で偶然発現するものしか知られておらず、その生成メカニズムは不明で、計画的に生成できる手法は知られていませんでした。つまり、実際に数値計算を行ってみないと非自明BICが存在するかどうかわからず、またフォトニック結晶の穴の大きさ・厚さ・屈折率などの構造パラメーターをどのように調節すれば非自明 BICが生成できるか明らかにされておらず、非自明なBICを実現する決定論的な手法が存在しませんでした

研究の成果

　今回NTT物性研と東工大は、誘電体周期構造（＝フォトニック結晶）を変形して対称性を変化するという非常に簡単な方法で、非自明なBICとなる光トポロジカル特異点を必ず生成できる方法を、世界で初めて見出しました。本成果では、誘電体薄膜に丸い穴が三角格子状に周期的に開けられたフォトニック結晶を用いますが、この構造はトポロジカル数が-2の自明なBIC（垂直方向BIC）を持つことが知られています（図3中央）。この構造を図3のように横方向または縦方向に引き延ばすことによって、自明な垂直方向の自明BICが二つに分裂して、トポロジカル数が-1の非自明な斜め方向BICが対で生成されることを理論的に示しました（図3左右）。また、フォトニック結晶の穴の形状を丸から三角形に変形することによって、トポロジカル数が半整数となり円偏光モードとなる別種のトポロジカル特異点を生成することも発見しました（図4）。これらの操作は、元々6回回転対称性^*4を持っていた三角格子結晶の対称性を壊すことに相当し、2回回転対称性にすると斜め方向BICが発現し、3回回転対称性にすると円偏光モードが発現します。また、これらトポロジカル特異点をレーザ等の光デバイスに応用した場合の、光出力の方向は変形の度合いによって可変となります（図5）。つまり、構造の対称性の簡単な操作により、様々なトポロジカル特異点を自由に生成、消滅でき、その方向や偏光の特性を制御できることを示しています。 　従来の手法では、非自明な斜め方向BICは、フォトニック結晶を構成する材料の屈折率に応じて構造パラメーターが特定の領域にある場合のみしか存在せず、フォトニック結晶の構造を調節する必要がありました。それに対し、今回の手法では材料の屈折率や構造パラメーターの値に依らず、6回回転対称性を持つ構造に変形を加えることで必ず非自明なBICが生成可能となるため、幅広い材料に対して自在に光トポロジカル特異点を形成することが可能となります。

原理のポイント

1. トポロジカル数-2の自明な垂直方向BICを持つ構造をベースとして用いる
   垂直方向 BICのトポロジカル数はフォトニック結晶の持つ回転対称性によって決まります。多くの場合垂直方向BICのトポロジカル数は±1ですが、6回回転対称性を持つフォトニック結晶ではトポロジカル数が-2の垂直方向BICが存在できることが知られています（図3中央）。本成果ではこのトポロジカル数が-2の垂直方向BICに注目しました
2. ６回回転対称性を壊す変形を施す
   本成果では、1.のトポロジカル数が-2の垂直方向BICに6回回転対称性を壊す変形を加えることにより、非自明なトポロジカル特異点を形成します。従来、自明な垂直方向BICは、非自明な斜め方向BICとは成因が異なるため、垂直方向BICの角度は変更不可能と考えられていました。しかしこれはトポロジカル数が±1の場合のみであり、トポロジカル数が-2の垂直方向BICは、6回回転対称性を壊す変形によってBICの角度が変更可能であることを今回発見しました（図3左右）。これはトポロジカル数が-2の自明なBICが2つのトポロジカル数が-1の非自明なBICに分裂することを意味します。特異点が分裂する際にトポロジカル数の合計は保存することが知られていることから、トポロジカル数が-2のBICを用いることが大事なポイントとなります。自明なBICから非自明なBICを生成できること自体、これまで知られておらず本成果が初めて明らかにしたことです。自明なBICの存在とそのトポロジカル数はフォトニック結晶の対称性のみで決定され、材料の屈折率や構造パラメーターによりません。従ってこの手法を用いることでフォトニック結晶の構造パラメーターに依らず、フォトニック結晶を変形させるだけで必ず非自明なBICを生成することができます。

今後の展開

本手法を用いることで、非自明な斜め方向BICを幅広い材料や構造に対して容易に生成できることになるため、非自明なBICに基づく物理現象探索やデバイス応用に貢献できると考えています。特に、化合物半導体等の光利得を持った材料に対して本手法を適用することによって、図5のように出射方向やトポロジカルな性質に起因する特殊な偏光状態を自在に制御できるレーザなどの発光デバイスが実現できると考えられ、フォトニック結晶のトポロジカルな性質を反映した光出力を自在に制御できる新しい光制御デバイスの可能性も期待できます。

論文情報

Taiki Yoda and Masaya Notomi
“Generation and Annihilation of Topologically Protected Bound States in the Continuum and Circularly Polarized States by Symmetry Breaking”
Physical Review Letters (2020)

用語解説

※1 ... フォトニック結晶

屈折率の空間分布が光の波長と同程度の周期となっている構造を一般にフォトニック結晶と呼ぶ。多くの場合、半導体に数百ナノメートル程度の周期構造を人工的に形成したものである。フォトニック結晶中の光はバンド構造を形成し、固体中の電子と同じくバンド理論で記述される。

※2 ... トポロジカルフォトニクス

フォトニック結晶中の光のモードのトポロジカルな性質に関する研究を指す。

※3 ... 偏光状態

光の電場ベクトルの振動方向を表す。光の電場ベクトルは進行方向と垂直方向を向いており、電場の振動方向が一定である場合直線偏光と呼ばれる。電場の振動方向が円を描く場合は円偏光と呼ばれ、電場の振動方向が楕円を描く場合は楕円偏光と呼ばれる。

※4 ... 回転対称性

図形をある点を軸に回転させたときに元の図形と一致する場合、その図形は回転対称性を持つ。