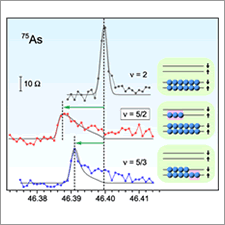
ＮＴＴ物性科学基礎研究所は、自然界の基本粒子^※1（フェルミ粒子、ボーズ粒子）とは異なる非アーベリアン準粒子^※2の存在が期待される電子状態を世界で初めて解明しました。

本成果では、NTTとJSTが独自に開発した高感度核磁気共鳴（NMR）法^※3により、5/2 分数量子ホール状態^※4（以下5/2状態）という非常に純度の高い半導体結晶中にお いてのみ実現される特殊な電子状態を測定することに成功いたしました。
今後、準粒子の実証実験を行い、エラー発生率が非常に低い新しい手法の量子計算（トポロジカル量子計算^※5）の応用を検討します。

なお、本成果は米国時間2012年1月26日（日本時間1月27日未明）に米国科学雑誌「Science」のオンライン速報版（Science Express）で公開されます。

本研究は、NTT(代表研究者：村木康二NTT物性科学基礎研究所主幹研究員)とJST(戦略的創造研究推進事業総括実施型研究(ERATO)「平山核スピンエレクトロニクスプロジェクト」(研究総括：平山祥郎東北大学教授) 物理研究・結晶成長グループ(グループリーダ：村木康二))の共同研究として行われました。

Science Express - 26 January 2012
Unraveling the Spin Polarization of the ν = 5/2 Fractional Quantum Hall State

⇒ニュースリリース
⇒量子固体物性研究グループ

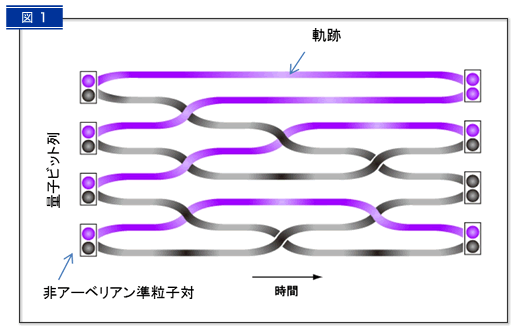
図１：トポロジカル量子計算のイメージ
トポロジカル量子計算^※5は、量子コンピュータで深刻な問題となる演算スケールの拡大に伴うエラー発生率の増加の問題を根本的に解決する方策として期待されています。それを現実のものとするためには、自然界の基本粒子とは異なる特異な性質をもった粒子（非アーベリアン準粒子^※2）が必要です。その存在には賛否両論あり、それを明確にするため、この準粒子が存在すると予想されている特殊な環境の電子状態を明らかにすることが課題となっていました。

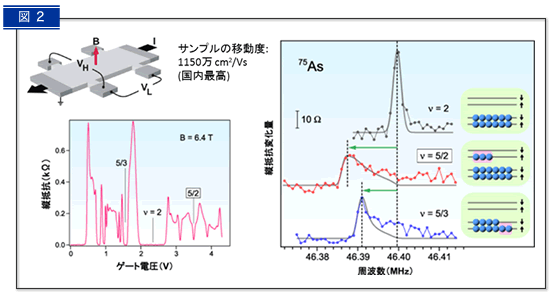
図2：高感度抵抗検出NMRによるスピン偏極の測定
非アーベリアン準粒子は、5/2分数量子ホール状態^※4という非常に純度の高い半導体結晶中で見られる特殊な電子状態において存在すると予想されています。本成果では、高移動度半導体結晶作製技術と、高感度抵抗検出核磁気共鳴(NMR)技術^※3により、この状態が完全スピン偏極であることを実証いたしました。これにより、5/2状態を説明するために提案されている理論は非アーベリアン準粒子の存在を肯定するものに絞られ、この準粒子が存在する可能性が非常に高くなりました。

※1 基本粒子
自然界の物質を構成する最小単位の粒子。電子などのフェルミ粒子と光子などのボーズ粒子に分類される。フェルミ粒子とボーズ粒子のちがいは、2つの同種粒子を入れ替えたときに、その量子力学的状態を記述する波動関数の符号が変化するかどうかによる。陽子、中性子、原子など、複数個の基本粒子から構成された粒子もフェルミ粒子かボーズ粒子に分類される。

※2 非アーベリアン準粒子
金属中の電子や結晶を構成する原子など、多くの粒子が関与することで全体としてあたかも一つの粒子のように振舞うことがあり、これを準粒子という。例として、半導体中の正孔や格子振動の量子であるフォノンなどがあるが、3次元空間ではこれら準粒子もフェルミ粒子かボーズ粒子に分類される。いっぽう2次元空間では、2つの準粒子を入れ替えたとき、波動関数に1でも‐1でもない複素数がかかることがあり、これをエニオンと呼ぶが、波動関数には位相の任意性があるため、準粒子を入れ替える前後で状態は変わらない。これに対し、2つを交換すると、元の状態とはちがう別の状態に変わってしまうという特異な性質を持った準粒子も理論的に予想されており、これを非アーベリアン準粒子（または非アーベリアンエニオン）という。

※3 核磁気共鳴(NMR)法
磁場中で原子核が固有の周波数で電磁波を共鳴吸収する現象。原子核の化学結合や周囲の電子の状態によって共鳴周波数がわずかに変化するため、分析や物性測定に使われる。共鳴周波数のシフト量は上向きスピンと下向きスピンの数の差に比例する。図2では、スピン状態のわかっている占有率2と5/3の状態と比較することで、5/2状態ではスピンの向きが揃っていることがわかる。

※4 5/2分数量子ホール状態
2次元空間に閉じ込められた電子に垂直に強い磁場を加えると、電子のエネルギーは「ランダウ準位」と呼ばれる離散的な準位に分裂する。電子が占めているランダウ準位の数を「占有率」といい、ギリシア文字のνであらわす。ホール効果はホールバーと呼ばれる形に加工した試料(図3)を用いて測定される。分数量子ホール効果は、低温で特定の占有率において縦抵抗（R_xx）がゼロとなりホール抵抗（R_xy）が普遍的な値h/e²（h：プランク定数、e:素電荷）のν^-1倍で一定となる現象で、その状態を分数量子ホール状態という。

※5 トポロジカル量子計算
複数の非アーベリアン準粒子が存在するときに準粒子の交換によって系の状態が変化することを論理ゲートとして用いた量子計算。空間に配置された準粒子を順番に入れ替えることで計算が実行される。計算結果は準粒子を交換する順序だけで決まり、経路の長さなどの詳細には依存しないため、エラー発生率を低く抑えることができるとされる。